|
|
Ejercicios
- Compruebe que la familia de rectas
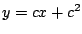 es solución
de la ecuación diferencial es solución
de la ecuación diferencial
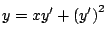 . Determine un valor de . Determine un valor de 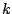 de forma que de forma que 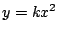 sea
una solución singular de la ecuación diferencial dada. Dibuje
en un mismo sistema de coordenadas la solución singular y
algunas soluciones particulares. sea
una solución singular de la ecuación diferencial dada. Dibuje
en un mismo sistema de coordenadas la solución singular y
algunas soluciones particulares.
- Compruebe que la familia de rectas
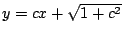 es
solución de la ecuación diferencial es
solución de la ecuación diferencial
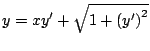 . Demuestre que el círculo . Demuestre que el círculo 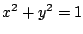 es una solución singular de la ecuación diferencial
dada. Dibuje en un mismo sistema de coordenadas la solución
singular y algunas soluciones particulares. es una solución singular de la ecuación diferencial
dada. Dibuje en un mismo sistema de coordenadas la solución
singular y algunas soluciones particulares.
- Compruebe que la familia de curvas
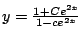 es solución de la ecuación diferencial es solución de la ecuación diferencial
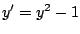 . Determine una solución singular para la
ecuación diferencial. Dibuje en un mismo sistema de coordenadas
la solución singular y algunas soluciones particulares. . Determine una solución singular para la
ecuación diferencial. Dibuje en un mismo sistema de coordenadas
la solución singular y algunas soluciones particulares.
- Compruebe que si
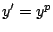 , donde , donde 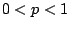 tiene
soluciones tiene soluciones tiene
soluciones tiene soluciones 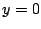 e e
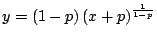 . Examine los casos especiales . Examine los casos especiales
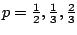 . Discuta la relación
entre estas soluciones. Existen otras soluciones además de las
dadas. Discuta los casos . Discuta la relación
entre estas soluciones. Existen otras soluciones además de las
dadas. Discuta los casos 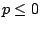 y y 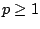 . .
- Revista virtual
Matemática, Educación e Internet -
ITCR
|