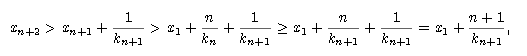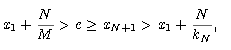1 2 3 4 5 6 7 8 9 10 11 12  

 
5. Apéndice

Faltó demostrar que la sucesión (kn)IN, construida en (d)(a), tiende a . He aquí la prueba, pero primero recordemos que

Bn = {  k IN | xn + 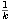no es cs de A  }    y    kn = minBn.

Notemos dos resultados preliminares. En primer lugar, que (kn) es creciente: Como xn+1 + 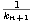no es cs de A, existe y A tal que

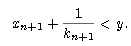
Y como claramente xn < xn+1, entonces xn + 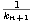< y, así que xn + 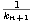no es cs de A; es decir, kn+1 Bn. Por último, como kn = minBn, debe ser kn kn+1. Por lo tanto la sucesión (kn) es creciente.

Y en segundo lugar, veamos por inducción que

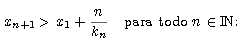
Para n = 1, es simplemente la definición de x2. Y si lo suponemos cierto para algún n, entonces:

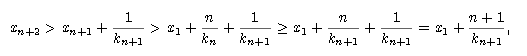
así que la afirmación vale también para n+1.

Ahora estamos listos para probar que kn 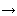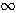. Sea M IR. Debemos probar que existe un N IN tal que 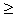n N 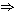kn > M. Podemos suponer que M > 0.

Tome cualquier cs c de A. Por arquimedianidad, existe un N IN tal que c - x1 < N 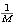 ; es decir, x1 + 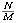> c. Como además xN+1 A y c es cs de A, y recordando la desigualdad que acabamos de probar, tenemos

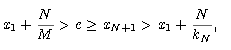
de donde concluimos que M < kN.

Y por último, como (kn) es creciente, resulta que kn 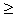kN > M para todo n 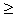N, como queríamos probar.

 
1 2 3 4 5 6 7 8 9 10 11 12

Revista Virtual, Matemática Educación e Internet.
Derechos Reservados.