|
3.4 Prueba de (e)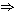 (a) (a)
Suponemos que IR es arquimediano con la propiedad de Cantor.
Sea i  IN. Tome una cs y de A; como IR es arquimediano, existe un k
IN. Tome una cs y de A; como IR es arquimediano, existe un k

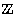 tal que y <
tal que y < 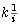 ,
de modo que k / i también es cs de A. Entonces el
conjunto { k ,
de modo que k / i también es cs de A. Entonces el
conjunto { k 
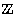 | k / i es cs de A } no es vacío. Sea ki
su mínimo (de modo que ki / i es cs de A
pero ( ki-1 ) / i no lo es).
| k / i es cs de A } no es vacío. Sea ki
su mínimo (de modo que ki / i es cs de A
pero ( ki-1 ) / i no lo es).
Ahora defina, para n = 1, 2, ...,
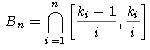
Veamos que Bn 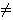 Ø: Como m = max{
Ø: Como m = max{ 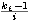 | i = 1, ...,n } no es cs de A, y M =
min{
| i = 1, ...,n } no es cs de A, y M =
min{ 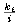 | i = 1, ... ,n } sí lo es, entonces m < M.
Así, Bn = [m, M]
| i = 1, ... ,n } sí lo es, entonces m < M.
Así, Bn = [m, M] 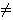 Ø.
Ø.
Ahora, por la propiedad de Cantor (es claro que (Bn) es
una sucesión decreciente de cerrados), la intersección B de los Bn
no es vacía. Además tiene sólo un punto, porque si x, y  B entonces
B entonces
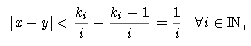
lo que por arquimedianidad implica que
| x - y | = 0; es decir, x = y.
Llamemos b a este único elemento de B, y veamos que b =
supA:
-
(i) Que b es cs de A:
Sea x > b. Por arquimedianidad existe i  IN tal que 1 < i ( x-b ), de donde sigue que 1/i
< x-b y entonces b < x - 1/i.
IN tal que 1 < i ( x-b ), de donde sigue que 1/i
< x-b y entonces b < x - 1/i.
Además, como b  B, debe ser ( ki - 1 ) / i
B, debe ser ( ki - 1 ) / i  b.
b.
Conectando las dos últimas desigualdades tenemos que
-
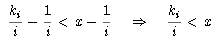
-
y como ki/i
es cs de A, se concluye que x 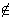 A,
A, 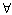 x > b.
x > b.
-
-
(ii) Sea  > 0. Que b -
> 0. Que b -  no es cs de A:
no es cs de A:
Por arquimedianidad existe i  IN tal que 1/i <
IN tal que 1/i <  .
Como b .
Como b  ki/i entonces
ki/i entonces
-
Y como (ki
-1) / i no es cs de A, b -  tampoco puede serlo.
tampoco puede serlo.
En conclusión, b = supA.
Comentarios: La idea
aquí es "encajar'' el extremo superior de A con intervalos
cuyos extremos derechos forman una sucesión decreciente de cotas de A
y cuyos extremos izquierdos forman una sucesión creciente de no-cotas de A,
ambas sucesiones convergiendo a un mismo punto que debe ser entonces la
frontera entre las cotas y las no-cotas; es decir, supA.
|