|
Veamos por último que b = supA:
-
(i) Que b es cs de A:
Sea c > b. Como kn
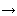 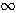 ,
existe n ,
existe n  IN tal que kn > 1 +
IN tal que kn > 1 + 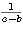 ;
luego ;
luego
c > b + 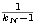 > xn + > xn +
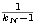 , ,
y como este último
número es cs de A, concluimos que c 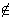 A,
A, 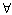 c > b.
c > b.
(ii) Sea  > 0. Que b -
> 0. Que b -  no es cs de A:
no es cs de A:
Como xn 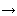 b, existe n
b, existe n  IN tal que |b - xn| <
IN tal que |b - xn| < ,
por lo que b - ,
por lo que b -  < xn.
< xn.
Como
xn  A, b -
A, b -  no puede ser cs de A.
no puede ser cs de A.
Por lo tanto, b = supA,
con lo que acaba la prueba.
Comentarios: Aquí se
construye una sucesión de Cauchy dentro de A, que crezca "lo
más rápido posible'', de la siguiente manera:
Se escoge x1  A. Si x1 + 1 no es cs de A, se escoge x2
A. Si x1 + 1 no es cs de A, se escoge x2
 A, mayor que x1 + 1; si x2 + 1 no es
cs de A se escoge x3
A, mayor que x1 + 1; si x2 + 1 no es
cs de A se escoge x3  A mayor que x2+1, y así se continúa. Cuando
A mayor que x2+1, y así se continúa. Cuando
xi + 1 sí sea cs de A, se prueba con xi
+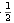 ,
xi + ,
xi + 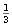 ,
etc, hasta encontrar un k tal que ,
etc, hasta encontrar un k tal que
xi + 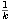 no sea cs de A y se pueda escoger xi+1 > xi
+
no sea cs de A y se pueda escoger xi+1 > xi
+ 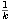 ,
pero tomando k lo menor posible para que el salto de xi
a xi+1 sea lo mayor posible. ,
pero tomando k lo menor posible para que el salto de xi
a xi+1 sea lo mayor posible.
Así se construye una sucesión (xn) cuyo límite es
mayor o igual que cualquier elemento de A, y como además la
sucesión está toda en A, su límite no puede ser mayor que ninguna cs
de A; esto es, lim xn = supA.
|