|
3.1 Prueba de (b)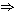 (a) (a)
Suponemos que IR es conexo.
La demostración es indirecta. Suponga que A no tiene extremo superior, y
considere
S = { x  IR | x no es cs de A }.
IR | x no es cs de A }.
Como A 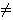 Ø, existe algún y
Ø, existe algún y  A, para el cual y-1
A, para el cual y-1  S. Entonces S
S. Entonces S 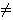 Ø.
Ø.
Además, veamos que S es abierto: Sea x  S. Por definición de S, x no es cs de A; por
lo tanto hay un y
S. Por definición de S, x no es cs de A; por
lo tanto hay un y  A tal que x < y. Entonces
A tal que x < y. Entonces
( La última inclusión se debe a que
como y  A, cualquier real menor que y no es cs de A.) Por lo
tanto x
A, cualquier real menor que y no es cs de A.) Por lo
tanto x 
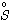 .
Como x .
Como x  S era arbitrario entonces S es abierto.
S era arbitrario entonces S es abierto.
Por aparte, considere
T = { x  IR | x es cs de A }.
IR | x es cs de A }.
Como A es acotado superiormente, T 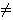 Ø.
Ø.
Veamos también que T es abierto: Si x  T entonces x es cs de A pero no es la menor (la menor
cota superior sería el extremo superior). De ahí que existe otro y
T entonces x es cs de A pero no es la menor (la menor
cota superior sería el extremo superior). De ahí que existe otro y  T tal que y < x. Entonces
T tal que y < x. Entonces
(La última inclusión se debe a que
como y es cs de A, cualquier real mayor que y es también
cs de A.)
Finalmente, es claro que IR = S 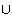 T y que S
T y que S 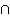 T = Ø. Es decir, IR es la unión disjunta de dos conjuntos abiertos, lo
cual contradice la suposición de que IR era conexo.
T = Ø. Es decir, IR es la unión disjunta de dos conjuntos abiertos, lo
cual contradice la suposición de que IR era conexo.
Comentarios: Aquí la
idea es que si A no tiene extremo superior, en el lugar donde éste
estaría hay un espacio vacío. Es decir, la frontera entre el conjunto de
cotas superiores (que es T, a la derecha del espacio) y el conjunto de
no-cotas (S, a la izquierda), debería ser supA, pero no existe.
Esto da una disconexión de IR.
Por cierto, la demostración no necesitaba ser indirecta. Si hubiéramos
definido S y T como lo hicimos, igual probaríamos que S es
abierto. Pero entonces T, por ser el complemento no vacío de S,
no puede ser abierto. Por lo tanto algún b  T no es interior, por lo que pertenece a S. Con un pequeño
esfuerzo puede demostrarse que
T no es interior, por lo que pertenece a S. Con un pequeño
esfuerzo puede demostrarse que
b = supA.
|