|
6. Glosario
Acotado (conjunto):
-
(a) Si A está contenido en un conjunto ordenado X, se dice que A es acotado superiormente (inferiormente) si admite una cota superior (inferior) en X.
-
(b) Si A está contenido un un espacio métrico (X,d), entonces A es acotado si
{ d(x,y) | x, y
 A } es acotado superiormente en IR. A } es acotado superiormente en IR.
Campo -cuerpo- (totalmente) ordenado:
-
Se dice que (K, +, ×,  ) es un campo (totalmente) ordenado si (K, +, ×) es un campo en el sentido algebraico usual, (K, ) es un campo (totalmente) ordenado si (K, +, ×) es un campo en el sentido algebraico usual, (K,
 ) es un conjunto (totalmente) ordenado, y para todos los a, b, c ) es un conjunto (totalmente) ordenado, y para todos los a, b, c
 K se cumple: K se cumple:
-
-
(i) a  b b 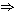 a + c a + c  b + c, y b + c, y
-
(ii) 0  a, 0 a, 0  b b 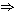 0 0  a × b. a × b.
Cota:
-
Si (X,  ) es un conjunto ordenado, c ) es un conjunto ordenado, c
 X y A X y A  X, entonces c es una cota superior (inferior) de A si para todo x X, entonces c es una cota superior (inferior) de A si para todo x
 A se cumple x A se cumple x  c (c c (c  x). x).
-
Extremo superior:
-
Si (X,  ) es un conjunto ordenado, b ) es un conjunto ordenado, b
 X y A X y A  X, entonces b es el extremo superior de X, entonces b es el extremo superior de
A (b = supA) si:
-
-
(i) b es cota superior de A, y
-
(ii) cualquier otra cota superior de A es mayor que b
(en IR, esta condición es equivalente a que 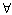  > 0, b-
> 0, b- no es cs de A).
no es cs de A).
Una formulación equivalente es decir que supA es la menor de las cotas superiores de A.
Ordenado (conjunto):
-
Si X es un conjunto y  es una relación reflexiva y transitiva en X × X, entonces (X, es una relación reflexiva y transitiva en X × X, entonces (X,
 ) es un conjunto preordenado. ) es un conjunto preordenado.
Si además  es antisimétrica entonces (X, es antisimétrica entonces (X,  ) es un conjunto ordenado. ) es un conjunto ordenado.
Y si además, para cualesquiera x, y  X se cumple x X se cumple x
 y ó y y ó y  x, entonces (X, x, entonces (X,  ) es totalmente ordenado. ) es totalmente ordenado.
-
Topología del orden:
-
Si (X,  ) es un conjunto totalmente ordenado, la topología del orden ) es un conjunto totalmente ordenado, la topología del orden
 en X es la generada por los conjuntos de la forma ]- en X es la generada por los conjuntos de la forma ]-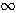 , a[ = { x , a[ = { x
 X | x < a } y los de la forma ]a, X | x < a } y los de la forma ]a,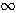 [ = { x [ = { x
 X | a < x }, para a X | a < x }, para a  X. X.
Es decir, los abiertos son las uniones de conjuntos de la forma ]a,b[ = { x
 X | a < x < b }, para a, b X | a < x < b }, para a, b
 X. X.
|