|
2. Algunos lemas
Antes de enunciar y probar el teorema que motiva este artículo, definamos nuestra posición. Olvidemos lo que sabemos de IR. Supongamos solamente que
IR es un cuerpo totalmente ordenado, y a partir de esto veamos "¿qué pasaría si
IR fuera completo, o conexo, o HB, etc.?'' Empecemos con unos lemas sencillos pero muy útiles.
Lema 1: Si A  IR, x es cota superior (cs) de A, y x
IR, x es cota superior (cs) de A, y x A, entonces existe supA y es igual a x.
A, entonces existe supA y es igual a x.
Prueba:
Por estar x en A, x es menor que cualquier otra cota superior de A. Es decir,
x es la menor de las cotas superiores de A.
Lema 2: Sea A  IR. Si
IR. Si 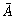 tiene extremo superior, entonces también A lo tiene y los dos son iguales.
tiene extremo superior, entonces también A lo tiene y los dos son iguales.
Prueba:
-
(i) Que sup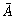 es cs de A: Inmediato, porque
A
es cs de A: Inmediato, porque
A  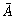 . .
-
(ii) Sea  > 0. Que sup
> 0. Que sup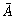 -
-  no es cs de A:
no es cs de A:
Como sup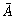 -
-  /2 no es cs de /2 no es cs de 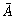 , existe
x , existe
x 
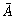 tal que
tal que
sup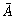 -
-  /2
< x. /2
< x.
Además, como x 
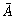 , hay un
y , hay un
y  A tal que
| x - y | < A tal que
| x - y | <  /2; es decir, tal que /2; es decir, tal que
-
-
Conectando las desigualdades obtenemos sup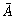 -
-  /2
< x < y + /2
< x < y +
 /2. /2.
Esto implica que sup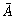 -
-  < y.
< y.
Por lo tanto, sup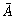 -
-  no es cs de A.
no es cs de A.
De los puntos (i) y (ii) se concluye que sup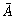 = sup A.
= sup A.
Lema 3: IR es arquimediano  IN
no es acotado superiormente. IN
no es acotado superiormente.
Prueba:
-
"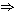 ":
Para cada y ":
Para cada y  IR existe un n
IR existe un n  IN tal que y < n · 1 = n (tomando x = 1 en la
definición de arquimedianidad). Esto quiere decir que ningún y
IN tal que y < n · 1 = n (tomando x = 1 en la
definición de arquimedianidad). Esto quiere decir que ningún y  IR es cs de IN.
IR es cs de IN.
-
"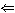 ":
Sean x, y ":
Sean x, y  IR con 0 < x. Como IN no es acotado superiormente, y / x no
es cs de IN, por lo que existe n
IR con 0 < x. Como IN no es acotado superiormente, y / x no
es cs de IN, por lo que existe n  IN tal que y/x < n, y de aquí que y < n · x.
IN tal que y/x < n, y de aquí que y < n · x.
|