|
3.2 Prueba de (c)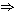 (a) (a)
Suponemos que IR es HB.
Tome cualquier a  A y defina
A y defina
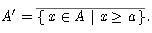
Entonces, como IR es HB, A' debe
ser compacto porque:
-
(i) Es obvio que A' es
cerrado.
(ii) A' es acotado superiormente por cualquier cota superior de A.
(iii) A' es acotado inferiormente por a, porque si b <
a entonces b < 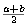 < a, y
< a, y
]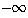 , ,
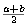 [
es un vecindario de b que no interseca { x [
es un vecindario de b que no interseca { x  A | x
A | x 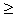 a }, de modo que b
a }, de modo que b 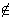 A'. A'.
Supongamos ahora que no existe supA'.
Entonces por el Lema 1 tenemos que
para cualquier x  A', x no es cs de A' y entonces hay un yx
A', x no es cs de A' y entonces hay un yx
 A' tal que x < yx.
A' tal que x < yx.
Ahora es claro que { ]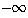 ,
yx[ | x ,
yx[ | x  A' } es un cubrimiento abierto de A', y por compacidad
existen x1, x2, ..., xn
A' } es un cubrimiento abierto de A', y por compacidad
existen x1, x2, ..., xn
 A' tales que
A' tales que
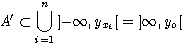
donde yo =
max{ yx1, ..., yxn
}. Pero esto último es contradictorio, porque yo
pertenece a A' pero no a ]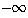 ,yo[. ,yo[.
Luego, A' debe tener extremo superior, y según el Lema 2
también A debe tenerlo, como queríamos probar.
Comentarios: Sabemos
que A es acotado superiormente. Si también lo fuera inferiormente, su
adherencia sería compacta. En todo caso, "recortamos" A
en cualquier punto y eliminamos todo a la izquierda de ese punto. Lo que queda
es acotado superior e inferiormente, y su adherencia es lo que denotamos A',
compacto. Y los subconjuntos compactos de IR deben tener extremo
superior: si no, cada x  A', por no ser cota, tendría un vecindario abierto que se extendería a
la derecha de x pero sin "salirse a la derecha'' de A'.
Esto daría un cubrimiento abierto de A' sin cubrimiento finito,
contradiciendo la compacidad de A'.
A', por no ser cota, tendría un vecindario abierto que se extendería a
la derecha de x pero sin "salirse a la derecha'' de A'.
Esto daría un cubrimiento abierto de A' sin cubrimiento finito,
contradiciendo la compacidad de A'.
|