|
3.3 Prueba de (d)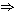 (a) (a)
Suponemos que IR es completo y arquimediano.
Tome cualquier x1  A y construya inductivamente la sucesión (xn)
A y construya inductivamente la sucesión (xn)
 A:
A:
-
(i) Si xn
es cs de A, entonces xn =
supA por el Lema 1.
Con esto termina la prueba.
(ii) Si xn
no es cs de A, sea y  A tal que xn < y.
Entonces 0 < y - xn , y por
arquimedianidad existe k
A tal que xn < y.
Entonces 0 < y - xn , y por
arquimedianidad existe k  IN tal que 1 < k ( y - xn ),
de donde
IN tal que 1 < k ( y - xn ),
de donde 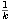 <
y - xn por lo que <
y - xn por lo que
- xn +
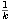 < y
< y
-
Entonces xn
+ 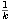 no es cs de A, y de ahí que el conjunto
no es cs de A, y de ahí que el conjunto
Bn
= { k  IN | xn +
IN | xn + 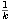 no es cs de A }
no es cs de A }
no es vacío. Sea kn
= min Bn, y sea xn+1
un elemento de A tal que
xn + 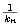 < xn+1.
< xn+1.
Si la condición (i) se
cumple para algún n IN, la prueba termina. Si no, se obtienen dos sucesiones: (xn)
IN, la prueba termina. Si no, se obtienen dos sucesiones: (xn)
 A y (kn)
A y (kn)  IN. La primera es claramente creciente, y la última tiende a
infinito (vea la prueba en el Apéndice).
Entonces podemos probar que (xn) es de
Cauchy:
IN. La primera es claramente creciente, y la última tiende a
infinito (vea la prueba en el Apéndice).
Entonces podemos probar que (xn) es de
Cauchy:
En efecto, sea  > 0. Como kn
> 0. Como kn 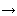 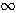 , existe N
, existe N IN tal que kN > 1 +
IN tal que kN > 1 + 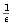 ,
o bien ,
o bien 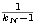 < <  . .
Por la definición de kN resulta que xN
+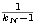 sí es cs de A, y entonces para todo n > N
tenemos
sí es cs de A, y entonces para todo n > N
tenemos
xN < xn
< xN + 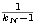 (porque xn
(porque xn  A). Por lo tanto
A). Por lo tanto
| xn
- xm | < 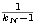 < <

para cualesquiera n, m
> N, lo que demuestra que la sucesión (xn)
es de Cauchy.
Ahora, como suponemos que IR es completo, (xn)
debe converger; sea b = lim xn. Como (xn)
es creciente, xn < b para todo n.
|