|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15
16 17
18 19 20
21
22 23 24
25
Algoritmo de clasificación jerárquica ascendente
La construcción de un árbol que representa a una jerarquía
indexada, con el algoritmo de clasificación jerárquica
ascendente (CJA), es un proceso recursivo que comienza con:
- a)
- la lista
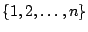 de enteros o símbolos con los cuales se representan los elementos de de enteros o símbolos con los cuales se representan los elementos de 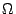 , y la
representación por lista
de los nodos de la partición en los conjuntos unitarios de , y la
representación por lista
de los nodos de la partición en los conjuntos unitarios de 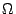 ; ;
- b)
- una matriz de disimilitudes
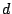 entre los objetos de entre los objetos de 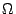 ; y ; y
- c)
- un criterio de agregación
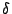 , ,
y produce en cada paso una nueva partición de
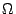 , por unión de las clases más cercanas de la partición
anterior: , por unión de las clases más cercanas de la partición
anterior:
- Paso 1
- (Inicialización)
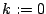
-
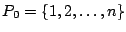 es la lista
de los nodos que representan a las clases de la partición
inicial {{1},{2},...,{n}}. es la lista
de los nodos que representan a las clases de la partición
inicial {{1},{2},...,{n}}.
-
![$d_0 =
\begin{array}[t]{r}
\{\{d(1,2),d(1,3),d(1,4), \ldots , d(1,p)\}, \\
\{d...
...\\
\ddots \ \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \\
\{d(n-1,p)\}\}
\end{array}.$](img115.png)
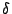 es una función de agregación. es una función de agregación.
- Paso 2
- Para
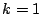 hasta hasta 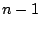 : :
-
Se determina 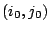 tal que tal que
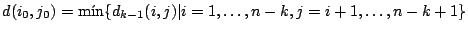 . .
- Se crea una nueva lista de los nodos
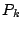 , eliminando de , eliminando de 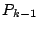 los
nodos los
nodos ![$P_{k-1}[i_0]$](img122.png) y y ![$P_{k-1}[j_0]$](img123.png) y añadiendo el nodo y añadiendo el nodo
![$\{d(i_0,j_0)+ kI,P_{k-1}[i_0], P_{k-1}[j_0]\}$](img124.png) . .
- Se crea una nueva matriz de disimilitudes
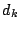 , eliminando de , eliminando de
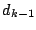 , las disimilitudes que corresponden a las clases eliminadas
y añadiendo las disimilitudes entre la clase que viene de ser
creada y las clases restantes. , las disimilitudes que corresponden a las clases eliminadas
y añadiendo las disimilitudes entre la clase que viene de ser
creada y las clases restantes.
|
![]()