Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15
16 17
18 19 20
21
22 23 24
25
Agregaciones
Además de la disimilitud, HierarchicalTree necesita que se
especifique un índice de agregación con el fin de construir la
jerarquía. El índice de agregación 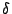 es una disimilitud
definida sobre el conjunto de partes de es una disimilitud
definida sobre el conjunto de partes de 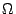 , sin que
necesariamente , sin que
necesariamente
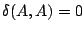 , para todo , para todo
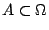 . .
Tabla 4:
Indices de agregación.
|
|
Las agregaciones que se encuentran en HierarchicalCluster se
muestran en la tabla 4. En estas definiciones, la
inercia de una clase 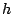 es la inercia respecto a su centro de
gravedad: es la inercia respecto a su centro de
gravedad:
donde 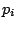 es el peso asociado al individuo es el peso asociado al individuo 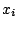 y y
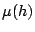 es el peso del conjunto es el peso del conjunto
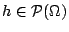 .
Se define también .
Se define también
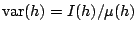 como la varianza de como la varianza de 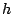 . .
En la implementación de las agregaciones anteriores, se supone que
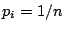 y y
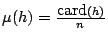 , y se usa la
fórmula de Lance, Williams & Jambu: , y se usa la
fórmula de Lance, Williams & Jambu:
Cada función MinDistance, MaxDistance, MeanDistance,
GravityCenter, IncreaseVariance,
Ward, JoinInertia, y JoinVariance está definida como una
función de nueve parámetros: las cardinalidades de 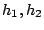 y
y 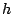 , (denotadas ca,cb,cc), las agregaciones , (denotadas ca,cb,cc), las agregaciones
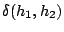 , , 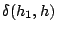 y y 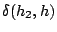 (denotadas
dab, dac, dbc) y los índices (denotadas
dab, dac, dbc) y los índices 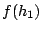 , , 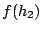 y y 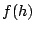 (denotados fa,fb,fc). Por ejemplo, en el caso de la
agregación de Ward, su
definición es:
(denotados fa,fb,fc). Por ejemplo, en el caso de la
agregación de Ward, su
definición es:
Ward[ca_,cb_,cc_,dab_,dac_,dbc_,fa_,fb_,fc_] :=
With[{abc = ca+cb+cc}, ((ca+cc)dac + (cb+cc)dbc - cc dab)/abc]
HierarchicalTree acepta como agregación cualquier
función de los nueve parámetros mencionados arriba; así, el
usuario puede especificar nuevos índices de agregación siempre
que respete el orden de los parámetros y que la evaluación sea
un número positivo.
|
![]()