Corte del árbol y definición de las clases

Una primera vista al gráfico parece definir cuatro clases, una de las cuales es unitaria. Sin embargo, para definir este número de clases se puede obtener más información del gráfico que produce HeightPlot. En él se muestran los valores que asumió la función de agregación Ward, en cada paso del algoritmo de clasificación jerárquica ascendente, al unir las dos clases más cercanas.

HeightPlot[A];

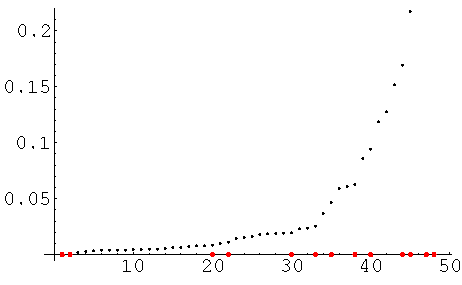
En este gráfico los últimos 7 puntos quedaron fuera de la región de graficación, lo cual es un efecto definido por omisión que procura un mejor detalle del comportamiento inicial del índice de agregación. Este efecto se puede eliminar utilizando la opción PlotRange->All.

HeightPlot[A,PlotRange->All];

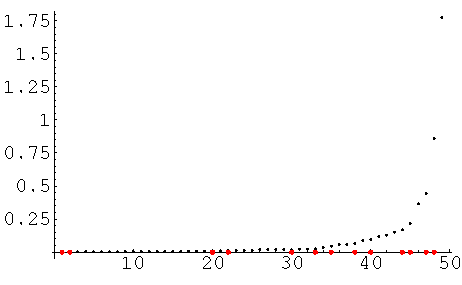
En el eje X, se marcan con puntos rojos, los pasos del algoritmo en los que el valor de la función de agregación produjo un incremento mayor que todos los anteriores. Estos valores pueden ser explícitamente obtenidos con la siguiente orden:

MaxJump[A]

El comando MaxJump[A]//TableForm despliega estos datos como una tabla con dos columnas.

Con la información de esta tabla y el gráfico anterior podría elegirse, por ejemplo, cortar el árbol en el nivel 45 definiendo 50 - 45 = 5 clases. El siguiente gráfico, muestra la parte superior de la jerarquía, si se corta al nivel 45. El número en el círculo de los nodos terminales corresponde a la cardinalidad de la clase que se define con el corte. Si el número no aparece encerrado por un círculo se trata de la etiqueta de un objeto e indica que la clase es unitaria compuesta sólo por ese objeto.

TreePlot[A, LevelCut -> 45, LeafLabelDistance -> 0.07];

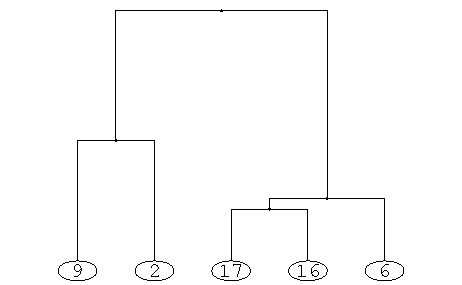
La siguiente orden muestra la composición de cada una de las clases de la partición resultante al cortar el árbol en el nivel 45 y define los símbolos P5 para identificar la partición completa y C1,C2,C3,C4 y C5 para cada una de sus clases:

P5 = {C1, C2, C3, C4, C5} = ClusterPartition[A, 45]