|
|
Ejercicios
- Resuelva cada una de las siguientes ecuaciones diferenciales
-
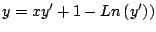
-
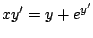
-
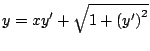
-
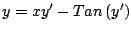
- Compruebe que la ecuación diferencial para la familia de
rectas
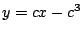 es es
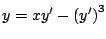 . .
- Compruebe que la ecuación diferencial
se reduce a una ecuación de Clairaut haciendo la sustitución
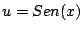 . .
- Una manera alternativa de definir la ecuación de Clairaut
es decir que es una ecuación de la forma
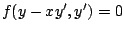 . .
- Compruebe que una familia de soluciones de la última
ecuación es
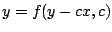 . .
- Use lo anterior para resolver la ecuación diferencial
- Revista virtual
Matemática, Educación e Internet -
ITCR
|