|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M.

1  2  3  4  5  6  7  8  9  10  11

 

 

 

Ecuaciones diferenciales homogéneas

Existen algunas ecuaciones diferenciales que al hacer un cambio de variable adecuado se reducen a ecuaciones en variables separadas, como el ejemplo anterior.

Antes de estudiar las ecuaciones diferenciales homogéneas es necesario definir lo que es una función homogénea.

 

	Definición  [Funciones homogéneas]
	Una función $f: D \subset \mbox{$\ I \hspace{-1.23mm} R $\ }^2 \rightarrow \mbox{$\ I \hspace{-1.23mm} R $\ }$ se dice homogénea de grado $n$ si $$f(tx,ty) = t^n f(x,y)$$ para todo $t > 0$ y todo $(x,y) \in D$.

 

Ejemplo

1. La función $f(x,y)= \frac{1}{\sqrt{x+y}}$ es homogéénea de grado $\frac{1}{2}$.

2. Las funciones $f(x,y)=e{\frac{x}{y} }$, $f(x,y)= \frac{x^2 - y^2}{x^2 + y^2}$, $f(x,y)=\frac{x}{2x+y}$ son homogéneas de grado 0.

3. Las funciones $f(x,y)= x^2 + y^2$, $f(x,y)=xy$, $f(x,y)=x^2-2xy+y^2$ son homogéneas de grado 2.

Ahora definimos lo que es una ecuación diferencial homogénea.

 

	Definición [Ecuación diferencial homogénea]
	Una ecuación diferencial ordinaria de primer orden, $y^{\prime} = f(x,y)$, es homogénea si la función $f(x,y)$ es homogénea de orden cero.

 

Observación: si la ecuación diferencial está escrita en la forma

$$M(x,y) dx + N(x,y) dy = 0$$

sería homogénea sí y sólo sí los coeficientes $M(x,y)$ y $N(x,y)$ son funciones homogéneos del mismo grado.

 

	Teorema
	Si la ecuación diferencial ordinaria de primer orden $$y^{\prime} = f(x,y)$$ es homogénea, entonces el cambio de variable $y=ux$ la reduce a una ecuación diferencial en variables separadas.

 

Demostración:

Al hacer la sustitución obtenemos

$$x u^{\prime} + u = f(x, x u)$$

Pero como $f(x,y)$ es una función homogénea de grado cero tenemos que

$$x \frac{du}{dx} + u = x^0 f(1,u)$$

de donde

$$x \frac{du}{dx} = f(1,u) - u \Rightarrow \frac{du}{f(1,u) - u} = \frac{dx}{x}$$

la cual es separable, como se quería.

 

Ejemplo

 
Resuelva la ecuación diferencial

$$\left(x^2 + y^2 \right) dx + xy dy = 0$$

La ecuación diferencial es homogénea pues $M(x,y) = x^2 + y^2$ y $N(x,y) = xy$ son homogéneas de grado dos

$$\begin{array}{rcl} M(tx,ty) & = & \left(t x \right)^2 + \l... ...\right) = t^2 \left( xy \right) = t^2 N(x,y) \\ \end{array}$$

Haciendo la sustitución

$$\begin{array}{rcl} \left(x^2 + \left(u x \right)^2 \right)... ... dx + \frac{u}{1 + 2 u^2} du \right) & = & 0 \\ \end{array}$$

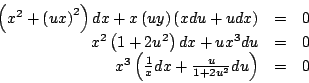
de donde

$$\frac{1}{x} dx + \frac{u}{1 + 2 u^2} du =0$$

Integrando y volviendo a las variables $x$ y $y$ obtenemos

$$Ln \mid x \mid + \frac{1}{4} Ln \mid 1 + 2 \left(\frac{y}{x} \right)^2 \mid = c \Rightarrow x^4 + 2 x^2 y^2 = c$$

Note que $x=0$ es una solución singular de la ecuación diferencial dada.

 

Observación: Cuando la ecuación diferencial homogénea está escrita en la forma

$$M(x,y) dx + N(x,y) dy = 0$$

conviene más rescribirla en la forma

$$\frac{dy}{dx} = -\frac{M(x,y)}{N(x,y)}$$

y aplicar quí el cambio de variable $y=ux$.

Ejemplo

Resuelva la ecuación diferencial

$$x y^{\prime} = \sqrt{x^2 - y^2 } + y$$

Factorizando $x$

$$y^{\prime} = \sqrt{1 - \left( \frac{y}{x} \right)^2} + \frac{y}{x}$$

Haciendo la sustitución $y=ux$

$$\frac{du}{\sqrt{1- u^2}} = \frac{dx}{x}$$

Integrando

$$ArcSen(u) = Ln \mid x \mid + Ln \mid c \mid$$

Y despejando $y$

$$\begin{array}{rcl} & \Rightarrow & arcsen\left( \frac{y}{x... ...& y = Sen \left(Ln \left( cx \right) \right) \\ \end{array}$$

Observación: al dividir por el factor $x \sqrt{1 - u^2}$ se pudo haber perdido algunas soluciones, pero $x=0$ no es solución y $1 - \frac{x^2}{y^2} =0 \Rightarrow y = \pm x$ que son soluciones singulares.

Subsecciones

• Ejercicios

 

 

Revista digital Matemática, Educación e Internet.