Ecuación lineal de primer orden

Tal vez, esta sea una de las ecuaciones diferenciales de mayor importancia, pues muchas de las aplicaciones que trataremos se modelan por medio de una ecuación de este tipo.

Definición [Ecuación lineal]

Una ecuación diferencial de primer orden que puede escribirse en la forma

$\begin{displaymath} \frac{dy}{dx} + P(x)y = Q(x) \end{displaymath}$

donde y son funciones reales, se llama ecuación diferencial lineal.

Observación: una ecuación diferencial lineal de orden tiene la forma

$\begin{displaymath} a_{n}(x) y^{(n)} + a_{n-1}(x) y^{(n-1)} + \dots + a_1(x) y^{\prime} + a_0(x) y = f(x) \end{displaymath}$

donde los coeficientes son funciones reales y $a_n(x) \neq 0$ . Note que cuando tenemos que

$\begin{displaymath} a_1(x) y^{\prime} + a_0(x)y = f(x) \end{displaymath}$

y al dividir por

$\begin{displaymath} y^{\prime} + \frac{a_0(x)}{a_1(x)} y = \frac{f(x)}{a_1(x)} \end{displaymath}$

La cual tiene la forma

$\begin{displaymath} y^{\prime} + P(x)y = Q(x) \end{displaymath}$

donde $P(x) = \frac{a_0(x)}{a_1(x)}$ y $Q(x) = \frac{f(x)}{a_1(x)}$ .

Teorema

La solución general de la ecuación diferencial de primer orden

$\begin{displaymath} \frac{dy}{dx} + P(x)y = Q(x) \end{displaymath}$
(1.10)

está dada por

$\begin{displaymath} y = e^{- \int P(x) dx} \left(\int Q(x) e^{\int P(x) dx } dx \right) \end{displaymath}$

Demostración
Reescribiendo la ecuación 1.10 como

$\begin{displaymath} \left(P(x) y - Q(x) \right) dx - dy = 0 \end{displaymath}$

podemos comprobar que $e^{\int P(x) dx}$ es un factor integrante. Multiplicando la ecuación 1.10 por este factor tenemos que

$\begin{displaymath} e^{\int P(x) dx } \frac{dy}{dx} + P(x)y = Q(x) \end{displaymath}$

de donde

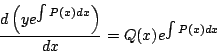
$\begin{displaymath} \frac{d \left(y e^{\int P(x) dx } \right) }{dx} = Q(x) e^{\int P(x) dx} \end{displaymath}$

e integrando respecto con

$\begin{displaymath} y e^{\int P(x) dx} = \int \left( Q(x) e^{\int P(x) dx} \right) dx \end{displaymath}$

como se quería.

Ejemplo:

Resolver la ecuación

$\begin{displaymath} x \frac{dy}{dx} - 4y = x^6 e^x \end{displaymath}$

Reescribiendo la ecuación tenemos

$\begin{displaymath} \frac{dy}{dx} - \frac{4}{x} y = x^5 e^x \end{displaymath}$

El factor integrante está dado por

$\begin{displaymath} \mu(x)= e^{-4 \int \frac{dx}{x} } = e^{-4 Ln(x)} = \frac{1}{x^4} \end{displaymath}$

Con lo cual la solución está dada por

$\begin{displaymath} \frac{y}{x^4} = \int x e^x dx = x e^x - e^x + c \end{displaymath}$

Es decir,

Ejemplo:

Considere la ecuación diferencial

$\begin{displaymath} x^ 2 y dx + \left( y^ 2 + x^ 2 p(x) \right) dy = 0 \end{displaymath}$

(1.11)

Encuentre una función de forma tal que la ecuación diferencial (1.11) sea exacta y resuelva dicha ecuación diferencial.

Para que la ecuación (1.11) sea exacta debe cumplir

$\begin{displaymath} \frac{\partial M}{\partial y} = x^2 = \frac{\partial N}{\partial x} = 2x P(x) + x^2 P^{\prime}(x) \end{displaymath}$

De aquí obtenemos la ecuación diferencial lineas en y

$\begin{displaymath} x^2 = 2x P(x) + x^2 P^{\prime}(x) \Rightarrow P^{\prime}(x) + \frac{2}{x} P(x) = 1 \end{displaymath}$

cuya solución es

$\begin{displaymath} P(x) = \frac{x}{3} + \frac{c}{x^2} \end{displaymath}$

De donde tomando obtenemos que $P(x)=\frac{x}{3}$ .

Ejemplo:
Compruebe que la ecuación diferencial

$\begin{displaymath} y^{\prime} + P(x) y = Q(x) y Ln(y) \end{displaymath}$

donde y son funcuiones reales, se transforma en una ecuación diferencial lineal al hacer .

Como

$\begin{displaymath} u = Ln(y) \Rightarrow u^{\prime} = \frac{y^{\prime}}{y} \Rightarrow y^{\prime} = u^{\prime} y = u^{\prime} e^{u} \end{displaymath}$

Sustituyendo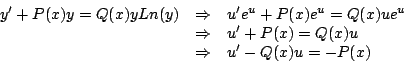

$\begin{displaymath} \begin{array}{rcl} y^{\prime}+ P(x) y = Q(x) y Ln(y) & \Ri... ... & \Rightarrow & u^{\prime} - Q(x) u = -P(x) \\ \end{array} \end{displaymath}$

la cual es una ecuación diferencial lineal.

Subsecciones

Ejercicios