|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M.

1  2  3  4  5  6  7  8  9  10  11

 

 

 

Factor integrante

Las ecuaciones diferenciales exactas son relativamente inestables, por decirlo de alguna manera, ya que la exactitud exige un balance en la forma de la ecuación diferemcial, balance que se destruye bajo pequeñas modificaciones, por ejemplo, la siguiente ecuación diferencial

$$\frac{y}{x^2} dx + \left(y - \frac{1}{x} \right) dy = 0$$ (1.3)

es exacta, pues

$$\frac{\partial M}{\partial y} = \frac{1}{x^2} = \frac{\partial N}{\partial x}$$

Sin embargo, al multiplicarla por el factor $x^2$, la ecuación /refedo2:eq1 se transforma en

$$y dx + \left( x^2y - x \right) dy = 0$$ (1.4)

la cual no es exacta.

Observación: podemos invertir la situación, al multiplicar la ecuación 1.4 por el factor $\frac{1}{x^2}$ obtenemos la ecuación diferencial 1.3, la cual es exacta. En tales circunstancias, es razonable preguntarse: ¿ hasta qué punto se puede convertir en exacta una ecuación diferencial que no lo es ?. En otras palabras, si la ecuación

$$M(x,y) dx + N(x,y) dy = 0$$

no es exacta, ¿ bajo qué condiciones se puede encontrar una función $\mu(x,y)$ con la propiedad de que

$$\mu(x,y) \left( M(x,y) dx + N(x,y) dy \right) = 0$$

sea exacta ?. Cualquier función que actúe de este modo se llama factor integrante. Así, $\frac{1}{x^2}$ es un factor integrante de la ecuación 1.4.

 

	Definición [Factor integrante]
	Si la ecuación diferencial $$M(x,y) dx + N(x,y) dy = 0$$ (1.5) no es exacta, pero al multiplicarla por el factor $\mu(x,y)$ se convierte en exacta, decimos que $\mu(x,y)$ es un factor integrante de la ecuación diferencial.

 

Ejemplo:
La expresión $\mu(x,) = xy^2$ es un factor integrante de la ecuación

$$\left(2y - 6x \right) dx + \left(3x - \frac{4x^2}{y} \right) dy = 0$$

pues al multiplicarla por $\mu(x,y)$ obtenemos la ecuación

$$\left(2xy^3 - 6x^2y^2 \right) dx + \left(3x^2y^2 - 4x^3y \right) dy = 0$$

La cual es exacta.

$$\frac{\partial M}{\partial y} = 6xy^2 - 12x^2y = \frac{\partial N }{\partial x}$$

El lector puede comprobar que la solución de ésta ecuación es $x^2y^3 - 2x^3y^2= c$.

De inmediato, la pregunta que surge es ¿ Cómo se encuentra un factor integrante ?, vamos a tratar de explorar un poco esta cuestióón. Si $\mu(x,y)$ es un factor integrante de la ecuacióón 1.5 entonces por el criterio de exactitud tenemos que

$$\frac{\mu(x,y) M(x,y) }{\partial y} = \frac{\mu(x,y) N(x,y)}{\partial x}$$

Aplicando la regla del producto, esto se reduce a la ecuación

$$M \frac{\partial \mu }{\partial y} - N \frac{\partial \mu}{... ...tial N}{\partial x} - \frac{\partial M}{\partial y} \right)$$ (1.6)

Pero despejar $\mu$ de la ecuación 1.6, es por lo general más difícil que resolver la ecuación original 1.5. Sin embargo, existen algunas excepciones importantes que podemos estudiar.

Suponga que la ecuación 1.5 tiene un factor integrante que depende solamente de $x$; es decir, $\mu = \mu(x)$. En este caso la ecuación 1.6 se reduce a

$$\frac{d \mu}{d x} = \left(\frac{\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x} }{ N } \right) \mu$$

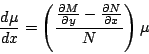
Separando variables obtenemos

$$\frac{d \mu}{ \mu} = \left(\frac{\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x} }{ N } \right) dx$$ (1.7)

Integrando a ambos lados de la expresión 1.7 podemos calcular fácilmente el factor integrante.

De manera análoga, si la ecuación 1.5 tiene un factor integrante que depende solamente de $y$, entonces la ecuación 1.6 se reduce a

$$\frac{d \mu}{d y} = \left(\frac{\frac{\partial N}{\partial y} - \frac{\partial M}{\partial x} }{ M } \right) \mu$$

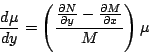
Separando variables obtenemos

$$\frac{d \mu}{ \mu} = \left(\frac{\frac{\partial N}{\partial y} - \frac{\partial M}{\partial x} }{ M } \right) dy$$ (1.8)

Integrando a ambos lados de la expresióón 1.8 podemos calcular fácilmente el factor integrante.

Este resultado se enuncia en el siguiente teorema.

 

Teorema

Si $$\frac{ \frac{\partial M}{\partial y} - \frac{\partial N}{ \partial x} }{N}$$ es continuo y depende solamente de $x$, entonces $$\mu(x) = exp\left( \int \left( \frac{ \frac{\partial M}{\pa... ...y} - \frac{\partial N}{ \partial x} }{ N } \right) dx \right)$$ es un factor integrante de la ecuación 1.5.   Si $$\frac{ \frac{\partial N}{\partial x} - \frac{\partial M}{ \partial y} }{ M }$$ es continuo y depende solamente de $y$, entonces $$\mu(y) = exp\left( \int \left( \frac{ \frac{\partial N}{\pa... ...l x} - \frac{\partial M}{ \partial y} }{M} \right) dx \right)$$ es un factor integrante de la ecuacióón 1.5.

 

Observación: al multiplicar por el factor integrante $\mu(x,y)$, podemos perder o ganar soluciones.

Es posible enunciar resultados similares al anterior para otros tipos de factores integrantes, el siguiente ejemplo muestra una situación de este tipo.

 

Ejemplo: Resolver la ecuación diferencial

$$\left( 3x +2y y^2 \right) dx + \left(x +4xy + 5 y^2 \right) dy = 0$$

si su factor integrante es de la forma $\mu(x,y)= \phi(x + y^2 )$.

Haga $z = x + y^2$ y calculemos las derivadas parciales de $\mu$ respecto a $x$ e $y$

$$\frac{\partial \mu}{\partial x } = \frac{d \mu}{\partial z} \frac{\partial z}{d x} = \frac{\partial \mu}{\partial z}$$

$$\frac{\partial \mu}{\partial y} = \frac{d \mu}{\partial z} \frac{\partial z}{d y} = 2y \frac{\partial \mu}{\partial z}$$

Sustituyendo en la ecuación 1.6 obtenemos que

$$\left(2y M - N \right) \frac{d \mu}{d z} = \left( \frac{\pa... ...l N }{\partial x} - \frac{\partial M}{\partial y} \right) \mu$$

Separando variables

$$\frac{d \mu}{\mu} = \left( \frac{ \frac{\partial N }{\partial x} - \frac{\partial M}{\partial y} }{ 2y M - N } \right) dz$$

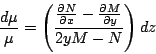
Como $M(x,y) = 3x +2y y^2$ y $N(x,y)= x +4xy + 5 y^2$, resulta que

$$\frac{d \mu}{\mu} = \frac{1}{x + y^2} dz = \frac{1}{z} dz$$

Integrando obtenemos que $\mu = z$. Es decir, que el factor integrante es $\mu(x,y) = x + y^2$. Al multiplicar por este factor tenemos que la ecuación original se convierte en

$$\left(3x^2 + 2xy + 4xy^2 + 2y^2 + 2y^3 + y^4 \right) dx + \left(x^2 + 4x^2y + 6xy^2 + 4xy^3 + 5y^4 \right) dy = 0$$

la cual es exacta y tiene como solución

$$x^3 + x^2y + 2x^2 y^2 + 2xy^3 + xy^4 + y^5 = c$$

Ejemplo:

 
Resuelva la siguiente ecuación diferencial

$$\left( xy^2 - y^3 \right) dx + \left(1 - xy^2 \right) dy = 0$$

Primero calculamos

$$\frac{\partial M}{\partial y} = 2xy - 3y^2 \hspace{2cm} \frac{\partial N}{\partial x}= -y^2$$

Ahora intentamos hallar un factor integrante que dependa únicamente de $x$ o de $y$, en este caso encontramos que depende de $y$.

$$g(y) = \frac{\frac{\partial M}{\partial y} - \frac{\partial... ...\frac{2y^2 -2xy}{y^2 \left( x - y \right)} = -\frac{2}{y}$$

Con lo cual el factor integrante esta dado por

$$\mu(y) = e^{ \int g(y) dy } = e^{-2 ln(y)} = \frac{1}{y^2}$$

Y al multiplicar la ecuación diferencial por este factor integrante obtenemos la ecuación

$$\left( x - y \right) dx + \left( \frac{1}{y^2} - x \right) dy = 0$$

la cual es exacta y tiene como solución

$$\frac{x^2}{2} - \frac{1}{y} - xy = c$$

Ejemplo

Halle los valores de $p$ y $q$ de forma tal que $\mu(x,y)=x^p y^q$ sea un factor integrante de la ecuación diferecnial

$$\left(2y^2+ 4x^2y \right)dx + \left( 4xy + 3x^3 \right)dy = 0$$ (1.9)

Si $\mu(x,y)=x^p y^q$ es un factor integrante entonces al multiplicar la ecuación diferencial (1.9) obtenemos que

$$\left( 2x^p y^{q+2} + 4x^{p+2} y^{q+1} \right)dx + \left( 4x^{p+1} y^{q+1} + 3x^{p+3}y^q \right) dy = 0$$

es una ecuación exacta, es decir, debe cumplir que

$$2 \left( q + 2 \right)x^p y^{q+1} + 4 \left( q + 1 \right) ... ... + 1 \right) x^p y^{q+1} + 3\left( p + 3 \right) x^{p+2} y^q$$

igualando coeficientes obtenemos el siguiente sistema de ecuaciones

$$\left \{ \begin{array}{rcl} 2 \left(q + 2 \right) & = & 4... ...ight) & = & 3 \left( p + 3 \right) \\ \end{array} \right.$$

el cual es equivalente a

$$\left \{ \begin{array}{rcl} 4p - 2q & = & 0 \\ 3p - 4q & = & -5 \\ \end{array} \right.$$

y tiene como solución $p=1$ y $q=2$, con lo cual el factor integrante es $\mu(x,y)=xy^2$ y la solución de la ecuación diferencial esta dada por

$$x^2y^4 + x^4y^3 = c$$

Subsecciones

• Ejercicios

 

 

Cidse - Revista virtual Matemática, Educación e Internet - ITCR