|
|
Ejercicios
- Resuelva cada una de las siguientes ecuaciones diferenciales
-
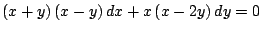
-
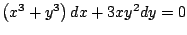
-
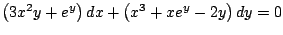
-
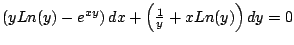
- Determine el valor de
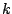 de modo que las siguientes ecuaciones sean exactas de modo que las siguientes ecuaciones sean exactas
-
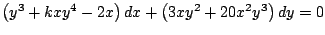
-
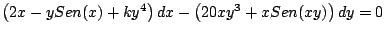
-
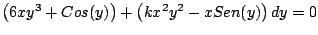
- Obtenga una función
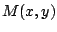 de forma que la ecuación
diferencial de forma que la ecuación
diferencial
sea exacta.
- Determine una función
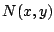 de manera que la ecuación
diferencial de manera que la ecuación
diferencial
sea exacta.
- Revista virtual
Matemática, Educación e Internet -
ITCR
|