|
|
Ejercicios
- Resuelva cada una de las siguientes ecuaciones diferenciales
-
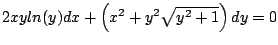
-
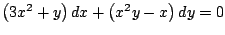
-
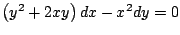
-
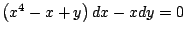
- Para las siguientes ecuaciones diferenciales encuentre un
factor integrante de la forma
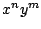 y resuelva la ecuación. y resuelva la ecuación.
-
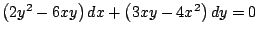
-
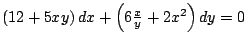
-
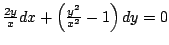
- Si
encuentre la solución de la ecuación diferencial
- Resolver la ecuación diferencial
haciendo el cambio de variable  , eligiendo un valor conveniente de , eligiendo un valor conveniente de 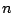 . .
- Revista virtual
Matemática, Educación e Internet -
ITCR
|