Revista   1 2 3 4  5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

El concepto del caos

Los matemáticos y los físicos vienen resolviendo ecuaciones diferenciales desde hace tres siglos, y, sin embargo, una de las peculiaridades más importantes de las soluciones a esas ecuaciones se había escapado a su comprensión hasta hace unos 15 años. Esto es más curioso en cuanto que esta peculiaridad, que se ha dado en llamar caos, es sumamente importante tanto práctica como teóricamente. El lector interesado en el tema del caos descubrirá que hoy en día la literatura es enorme. Citamos solamente algunas referencias representativas: para una introducción popularizada al caos en general, véase [6], para una introducción técnica a los temas fundamentales, [23], y para una avanzada en física, [8].

Explicaremos brevemente el caos. En la mecánica clásica se estudia el movimiento de partículas que interactúan entre sí de acuerdo a leyes dinámicas. Estas leyes se expresan por medio de ecuaciones diferenciales ordinarias. Frecuentemente los sistemas dinámicos son del tipo llamado autónomos de tiempo-contínuo de orden n. En este caso las ecuaciones son de la forma:

$${\frac{dx}{dt}}$$ (1)

donde x es un vector n-dimensional, f es una función   f : $$\Re^{n}_{}$$ $$\longmapsto$$ $$\Re^{n}_{}$$, y t es una variable que llamaremos el tiempo. Además, para poder resolver estas ecuaciones diferenciales, es necesario conocer las condiciones iniciales del sistema, que son de la forma x(t₀) = x₀, donde t₀ es el valor inicial del tiempo, y x₀ es un vector de constantes. Puede ser que exista una solución analítica cerrada que tenga un número finito de términos, pero, exceptuando los casos más sencillos y los triviales, éste nunca es el caso. Así que el recurso obligado es resolver el problema usando una computadora y métodos numéricos aproximados. El procedimiento a seguir en estos casos es discretizar el espacio y el tiempo, es decir, se toman segmentos finitos de las coordenadas de espacio y tiempo, y de estos se seleccionan algunos valores en los que se evalúan las variables dependientes. En este caso discretizaremos el tiempo en valores t_i, i = 0, 1, 2,..., N, donde t_N es el valor más grande que toma. Escogiendo la escala del tiempo adecuadamente se puede hacer $$\triangle$$t = 1,  y así obtenemos una de las posibles formulaciones utilizables en la programación de un sistema autónomo:

 

Dada una cierta disposición de las partículas, podría pensarse que si se variaran las condiciones iniciales ligeramente, por ejemplo, modificando en un milésimo a una de las condiciones iniciales, esta segunda solución sería parecida a la primera. En el caso específico de sistemas físicos, es natural que se pensara de este modo, pues este razonamiento obedece en parte a la fe en el principio de causalidad: supone que de algún modo la posición inicial es la ``causa" de la posición final, y consecuentemente, si la causa se modifica muy poco, pues el principio de causalidad diría que efecto va a ser casi el mismo. Sin embargo, esta suposición es totalmente falsa. Se llama caos precisamente a la observación, lograda inicialmente por medios computacionales, de que en cualquier sistema que no sea muy sencillo, el comportamiento cambia total y dramáticamente cuando se varían las condiciones iniciales en lo más mínimo. De hecho las trayectorias dadas por el vector x(t) con el paso del tiempo divergen exponencialmente en función de la diferencia en las condiciones iniciales. Llama la atención que no sea hasta nuestro tiempo que se haya llegado a esta comprensión, y sin embargo, si uno se pone a pensar lo difícil que es realizar cálculos aritméticos complicados a mano, y lo fácil que es equivocarse haciéndolos, se entiende que durante todos estos siglos lo que probablemente ha estado pasando ha sido que cuando alguien observaba el fenómeno al hacer los cálculos, lo achacaba a un error o al uso de un número insuficiente de cifras decimales; si lo veía en la naturaleza, lo achacaba a algún error experimental o de medición.

Paradójicamente, hay bastante orden en el caos. Los atractores extraños, a los cuales tienden las trayectorias caóticas, permiten llevar a cabo predicciones generales sobre el sistema. También en muchos sistemas hay leyes que se cumplen exactamente, como la conservación de la energía y del momentum y otras integrales que puedan tener las ecuaciones de movimiento en la mecánica clásica. Y algunos de los datos más importantes de un sistema a veces no están relacionados con la solución de las ecuaciones dinámicas. Por ejemplo, en el modelo Glashow-Weinberg-Salam de la física, que explica la relación entre las fuerzas electromagnéticas y las débiles, las predicciones más importantes están vinculadas con las masas de las partículas y la intensidad de las fuerzas mismas, no con las trayectorias de las partículas. En los sistemas biológicos la solución exacta teórica del sistema casi nunca es lo más importante, sino más bien la comprensión de como funciona el sistema en la realidad. Para terminar este breve resumen daremos algunos ejemplos de sistemas dinámicos autónomos. Una partícula sola en una dimensión obedece a dos ecuaciones del tipo (1), a saber:

$$\prime \prime$$

donde m es la masa de la partícula, y F(x) es una fuerza que actúa sobre la partícula. De estas ecuaciones se obtiene la ecuación de Newton para el movimiento de la partícula. Debido a la presencia de las dos variables x y v el espacio de fase es bidimensional. Una partícula aislada moviéndose en tres dimensiones espaciales tiene entonces un espacio de fase hexadimensional. Dos partículas interactuando entre sí tienen un espacio de fase de 12 dimensiones, 6 para cada una. Normalmente un sistema así no es caótico. Tres partículas interactuando entre sí tienen un espacio de fase de 18 dimensiones, y normalmente forman un sistema caótico, debido a que las fuerzas entre ellas llevan a ecuaciones no-lineales y complicadas. Sin embargo, no es necesario en absoluto que el espacio de fase tenga tantas dimensiones para que el sistema sea caótico, y ni siquiera tiene que ser no-lineal. Como ejemplo tomemos el sistema del circuito de Chua [16], que está dado por solamente tres ecuaciones autónomas simplemente lineales, aunque sí contiene algunas funciones de grada:

$$\prime \alpha$$ =

$$\prime$$ = x - y + z

$$\prime \beta$$ =

donde h es la función discontinua

f (x) = $$\left\{\vphantom{ \begin{array}{ll} m_1x+(m_0-m_1) & \mbox{si $x ... ... $-1\leq x\leq 1$}\\ m_1x-(m_0-m_1) & \mbox{si $x< -1$} \end{array} }\right.$$$$\begin{array}{ll} m_1x+(m_0-m_1) & \mbox{si $x >1$}\\ m_0x & \mbox{si $-1\leq x\leq 1$}\\ m_1x-(m_0-m_1) & \mbox{si $x< -1$} \end{array}$$

Naturalmente a estas tres ecuaciones corresponde un espacio de fase tridimensional.

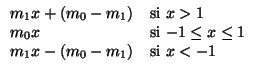
Revista   1 2 3 4  5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

Revista Matemáticas, Educación e Internet^â
Derechos Reservados