Ejercicios

Demuestre usando inducción, las propiedades de potenciación con exponentes naturales.

Usando las propiedades de potenciación con exponentes naturales, demuéstrelas para exponentes enteros.

Demuestre las propiedades de potenciación con exponentes racionales, usando las correspondientes a exponentes enteros.

De las siguientes expresiones, comente sobre cuales tienen sentido y cuales no:

0^-1 (- 1)³ (- 4)^1/2 (- 5)⁰ 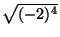$\sqrt{(-2)^{4}}$

De las siguientes igualdades, marque las que son verdaderas

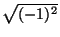$\sqrt{(-1)^{2}}$ = - 1 5⁰ = 0 4^-2 = - 16 9^1/2 =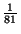 ${\frac{1}{81}}$

Simplifique las siguientes expresiones

$\begin{array}[c]{cc}%% \;\;\;\;\;\frac{a^{2}b}{ab^{-2}},\;\;\; & \frac{\left( ... ...3}},\;\;\;\;\left( \sqrt[3]{a^{5}b\sqrt{a^{2}b^{4}c}}\right) ^{6}%% \end{array}$

Resuelva las siguientes ecuaciones exponenciales para x 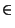$\in$ IQ:

$\displaystyle \begin{array}[c]{lllll}%% 2^{x+1}=4 & 3^{-x+1}=9^{x} & 2^{x+3}=\l... ...=4 & 8^{3x-1}=16^{2x+1} & 4^{x}=3\cdot2^{x+1}-8 & x^{x}=\sqrt{x}. & \end{array}$

Resuelva las siguientes ecuaciones

$\displaystyle \begin{array}[c]{ccccc}%% \sqrt[3]{x}-3\sqrt[6]{x}+2=0 & & 2x^{6}... ...{x}+9\sqrt[6]{x}+14=0 & & 2x^{4}+11x^{2}=6 & & x^{4/3}-x^{2/3}-1=0. \end{array}$

Si a > 0, demuestre con detalle que a^r > 0 para todo r 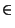$\in$ IQ.

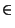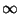Demuestre que para r $\in$ IQ⁺ se tiene que la función f (x) = x^r es creciente en [0, $\infty$ [.

Si n $\in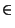$ IN es impar, demuestre que f (x) = xⁿ define una función estrictamente creciente en IR. Además f es biyectiva. ¿Cuál es su inversa?

Si n es par, entonces f = IR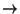^- $\rightarrow$ IR⁺, definida por f (x) = xⁿ, es biyectiva y estrictamente decreciente. ¿Cuál es su inversa?

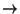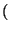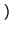Si 0 < a < 1, demuestre que la función f : IQ $\rightarrow$ IR, definida por f $\left(\vphantom{ r}\right.$ r $\left.\vphantom{ r}\right)$ = a^r, es estrictamente decreciente. En particular aⁿ < a para cada n 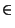$\in$ IN.

Demuestre usando el principio de inducción que si 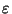$\varepsilon$ > 0 se tiene

$\displaystyle \left(\vphantom{ 1+\varepsilon}\right.$ 1 + $\displaystyle \varepsilon$ $\displaystyle \left.\vphantom{ 1+\varepsilon}\right)^{n}_{}$ > 1 + n $\displaystyle \varepsilon$ + $\displaystyle {\textstyle\frac{1}{2}}$ n $\displaystyle \left(\vphantom{ n-1}\right.$ n - 1 $\displaystyle \left.\vphantom{ n-1}\right)$ $\displaystyle \varepsilon^{2}_{}$ , $\displaystyle \forall$ n $\displaystyle \in$ IN.

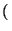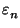
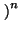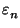Concluya que la sucesión $\left(\vphantom{ \sqrt[n]{n}}\right.$ $\sqrt[n]{n}$ $\left.\vphantom{ \sqrt[n]{n}}\right)_{n\in I\!\! N}^{}$ converge a 1. Sug. n = $\left(\vphantom{ 1+\varepsilon_{n}}\right.$ 1 + $\varepsilon_{n}^{}$ $\left.\vphantom{ 1+\varepsilon_{n}}\right)^{n}_{}$ , donde $\varepsilon_{n}^{}$ = $\sqrt[n]{n}$ - 1 > 0.