|
|
| Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
![]()
=
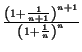 =
= ![]()
![]()
![]()
![]() 1 +
1 + ![]()
![]()
=
![]() 1 -
1 - ![]()
![]()
![]() >
> ![]() 1 -
1 - ![]()
![]()
![]()
=
![]() > 1,
> 1,
para todo
n ![]() IN. En el segundo renglón, hemos hecho uso de la
desigualdad de Bernoulli, con
x = -
IN. En el segundo renglón, hemos hecho uso de la
desigualdad de Bernoulli, con
x = - ![]() > - 1. Esto demuestra que
la sucesión
> - 1. Esto demuestra que
la sucesión
![]() xn
xn![]() es creciente. Similarmente se
demuestra que la sucesión
es creciente. Similarmente se
demuestra que la sucesión
![]() yn
yn![]() es decreciente. En
efecto, el lector puede verificar que
es decreciente. En
efecto, el lector puede verificar que
Prueba
Tomemos
x ![]() IR y definamos n = [x]. Tenemos entonces
n
IR y definamos n = [x]. Tenemos entonces
n ![]() x < n + 1,
y consecuentemente
x < n + 1,
y consecuentemente
![$\displaystyle \left.\vphantom{ 1+\frac{1}{x}}\right)^{x-[x]}_{}$](img701.gif) < 1 +
< 1 + ![$\displaystyle \left.\vphantom{ 1+\frac{1}{x}}\right)^{x-[x]}_{}$](img701.gif) = 1.
= 1.
![$\displaystyle \left.\vphantom{ 1+\frac{1}%%
{x}}\right)^{x-[x]}_{}$](img703.gif) = e.
= e.