Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28 

Ejercicios

  1. Muestre usando el principio de inducción que:

    1 + $ {\frac{1}{2}}$ + ... + $ {\frac{1}{2^{n}}}$ = 2 - $ {\frac{1}{2^{n}}}$, n $ \in$ IN.

    1 + r + ... + rn = $ {\frac{1-r^{n+1}}{1-r}}$, n $ \in$ IN, r $ \neq$ 1.

  2. Muestre por inducción que f (x) = xn es estrictamente creciente en [0,$ \infty$[, para todo n $ \in$ IN.

  3. Sea x > - 1. Use el principio de inducción para demostrar la desigualdad de Bernoulli:

    (1 + x)n $\displaystyle \geq$ 1 + nx,$\displaystyle \forall$n $\displaystyle \in$ IN.

  4. Sea x $ \in$ IR. Demuestre que existe un único k $ \in$ IZ tal que k $ \leq$ x < k + 1 (ya se demostró la existencia en el caso x > 0).

  5. Usando la definición, y el principio de inducción, demuestre que para m, n $ \in$ IN y a, b $ \in$ IR * se tiene

    aman = am + n,  $\displaystyle \left(\vphantom{ ab}\right.$ab$\displaystyle \left.\vphantom{ ab}\right)^{n}_{}$ = anbn,  $\displaystyle \left(\vphantom{ a^{n}}\right.$an$\displaystyle \left.\vphantom{ a^{n}}\right)^{m}_{}$ = amn.

  6. Muestre usando el principio de inducción que para todo n $ \in$ IN se tiene:

    $\displaystyle \sum\limits_{k=0}^{n}$n2 = $\displaystyle {\frac{n}{6}}$(n + 1)(2n + 1),        $\displaystyle \sum\limits_{k=0}^{n}$n3 = $\displaystyle {\frac{n^{2}}{4}}$(n + 1)2.

  7. Muestre que n2 + 3n + 1 es impar para todo n $ \in$ IN.

  8. Muestre que 2n - 3 $ \leq$ 2n - 2 para todo n $ \geq$ 5.

  9. Muestre que para n $ \in$ IN * se tiene

    1 + 3 + 5 +...+ (2n - 1) = n2.

    Calcule 1 + 3 + 5 +...+ 99.

  10. Muestre que 11n - 4n es divisible por 7, para todo n $ \in$ IN.

  11. Muestre que an - bn es divisible por a - b, para todo n $ \in$ IN y a, b $ \in$ IN, a > b.

  12. Demuestre por inducción que para n $ \in$ IN se tiene:

    (a)
    52n - 1 es divisible por 8.

    (b)
    5n - 4n - 1 es divisible por 16.

  13. Para los siguientes conjuntos, demuestre que son acotados superiormente, y halle el supremo:

    A = $\displaystyle \left\{\vphantom{ x\in I\!\! Q:1\leq x<3}\right.$x $\displaystyle \in$ IQ : 1 $\displaystyle \leq$ x < 3$\displaystyle \left.\vphantom{ x\in I\!\! Q:1\leq x<3}\right\}$,  B = $\displaystyle \left\{\vphantom{ 1-\frac{1}%% {n}:n\in I\!\! N}\right.$1 - $\displaystyle {\frac{1}{n}}$ : n $\displaystyle \in$ IN$\displaystyle \left.\vphantom{ 1-\frac{1}%% {n}:n\in I\!\! N}\right\}$,  C = $\displaystyle \left\{\vphantom{ x\in I\!\! Q:x^{2}<3}\right.$x $\displaystyle \in$ IQ : x2 < 3$\displaystyle \left.\vphantom{ x\in I\!\! Q:x^{2}<3}\right\}$.

  14. Demuestre que el axioma del extremo superior implica la versión 1 del axioma de completitud.

  15. Considere B $ \subseteq$ IR no vacío. Decimos que B es acotado inferiormente si existe a $ \in$ IR tal que a $ \leq$ y para todo y $ \in$ B. En tal caso se dice que a es una cota inferior de B. Demuestre que si B es acotado inferiormente, existe una cota inferior máxima para B. Esto es, existe $ \beta$ $ \in$ IR tal que:

    (a)
    $ \beta$ es cota inferior de B.

    (b)
    Si a es cota inferior de B, entonces a $ \leq$ $ \beta$.

    Tal $ \beta$ se llama el extremo inferior de B, y se denota $ \beta$ = inf B. Sug. El conjunto

    A = $\displaystyle \left\{\vphantom{ a\in I\!\! R:a\mbox{ es cota inferior de }B}\right.$a $\displaystyle \in$ IR : a es cota inferior de B$\displaystyle \left.\vphantom{ a\in I\!\! R:a\mbox{ es cota inferior de }B}\right\}$

    es acotado superiormente.

  16. Si x < y, n $ \in$ IN, demuestre que existen al menos n racionales entre x y y (use inducción). Concluya que existe un número infinito de racionales entre x y y.

  17. Si n $ \in$ IN y x, y $ \in$ IR, demuestre que

    xn - yn = (x - y)$\displaystyle \left(\vphantom{ x^{n-1}+x^{n-2}y+\cdots+xy^{n-2}+y^{n-1}}\right.$xn - 1 + xn - 2y + ... + xyn - 2 + yn - 1$\displaystyle \left.\vphantom{ x^{n-1}+x^{n-2}y+\cdots+xy^{n-2}+y^{n-1}}\right)$.

    Puede usar el ejercicio 1.

  18. Demuestre que $ \sqrt{3}$, $ \sqrt{5}$, $ \sqrt{6}$ son irracionales. En general, demuestre que $ \sqrt{p}$ es irracional, si p es primo. Se puede demostrar que $ \sqrt{n}$ es irracional, siempre que n $ \in$ IN no sea cuadrado perfecto.

  19. Si a es racional y b irracional, demuestre que a + b es irracional. En particular, - b es irracional. [Sug. La suma de racionales es racional]. ¿Qué pasa con la suma si ambos a y b son irracionales?

  20. Si a $ \neq$ 0 es racional y b irracional, demuestre que ab, ab-1 son irracionales. En particular, b-1 es irracional. [Sug. Producto y división de racionales es racional]. ¿Qué pasa con el producto si ambos a y b son irracionales?

  21. Use el ejercicio anterior, y la densidad de IQ, para demostrar que el conjunto de los números irracionales es denso en IR.

  22. Dé un ejemplo de dos números irracionales, tales que su suma y su producto sean ambos racionales.

  23. Demuestre que $ \sqrt[3]{2}$ y $ \sqrt{2}$ + $ \sqrt{3}$ son irracionales.

  24. Estudie la convergencia de las siguientes sucesiones. En caso convergente, halle el límite:

    an = $\displaystyle {\frac{n}{n+1}}$ - $\displaystyle {\frac{n+1}{n}}$ an = cosn$\displaystyle \pi$ an = n(- 1)n
    an = 1 + (- 1)n an = 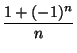$\displaystyle {\frac{1+(-1)^{n}}{n}}$ an = $\displaystyle {\frac{(-1)^{n}}{n}}$ + (- 1)n
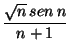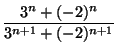    an = $\displaystyle {\frac{\sqrt{n}\, sen \,n}{n+1}}$ an = $\displaystyle {\frac{3^{n}+(-2)^{n}}{3^{n+1}+(-2)^{n+1}}}$ an = 1 + $\displaystyle {\frac{n}{n+1}}$cos$\displaystyle {\frac{n\pi}{2}}$

  25. Estudie la convergencia. En caso convergente obtenga el límite.

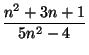    an = $\displaystyle {\frac{n^{2}+3n+1}{5n^{2}-4}}$,    cn = $\displaystyle {\frac{1}{n}}$$\displaystyle \left[\vphantom{ {\frac{n^{2}}{3}}}\right.$$\displaystyle {\frac{n^{2}}{3}}$$\displaystyle \left.\vphantom{ {\frac{n^{2}}{3}}}\right]$,    bn = sen$\displaystyle \left(\vphantom{ {\frac{n\pi}{4}}}\right.$$\displaystyle {\frac{n\pi}{4}}$$\displaystyle \left.\vphantom{ {\frac{n\pi}{4}}}\right)$.

  26. Sea $ \left(\vphantom{ x_{n}}\right.$xn$ \left.\vphantom{ x_{n}}\right)$ definida por

    x1 = 2,  xn + 1 = $\displaystyle \sqrt{2x_{n}+4}$,  $\displaystyle \forall$n $\displaystyle \geq$ 1.

    Muestre por inducción que esta sucesión es creciente y acotada superiormente por M = 4. Concluya que $ \left(\vphantom{ x_{n}}\right.$xn$ \left.\vphantom{ x_{n}}\right)$ es convergente y halle el límite.

  27. Si an $ \rightarrow$ $ \infty$, demuestre que $ {\frac{a_{n}}{1+a_{n}%% }}$ $ \rightarrow$ 1.

  28. Suponga que an $ \rightarrow$ 0, y que an > 0 para todo n. Demuestre que $ \left(\vphantom{ \frac{1}{a_{n}}}\right.$$ {\frac{1}{a_{n}}}$$ \left.\vphantom{ \frac{1}{a_{n}}}\right)$ diverge a infinito.

  29. Estudie la convergencia:

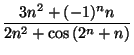    an = $\displaystyle \left[\vphantom{ {\frac{n}{2}}}\right.$$\displaystyle {\frac{n}{2}}$$\displaystyle \left.\vphantom{ {\frac{n}{2}}}\right]^{1/n}_{}$,    bn = $\displaystyle {\frac{3n^{2}+(-1)^{n}n}{2n^{2}+\cos\left( 2^{n}+n\right) }}$,      cn = $\displaystyle \left(\vphantom{ 1+{\frac{1}{n}}}\right.$1 + $\displaystyle {\frac{1}{n}}$$\displaystyle \left.\vphantom{ 1+{\frac{1}{n}}}\right)^{n^{2}}_{}$.

  30. Demuestre, utilizando la definición, la convergencia de las sucesiones:

    an = $\displaystyle {\frac{n}{n+1}}$,    bn = $\displaystyle {\frac{1}{n}}$$\displaystyle \left[\vphantom{ \frac{n}{2}}\right.$$\displaystyle {\frac{n}{2}}$$\displaystyle \left.\vphantom{ \frac{n}{2}}\right]$,    cn = $\displaystyle {\frac{1}{n}}$cos$\displaystyle {\frac{n\pi}{2}}$,    dn = $\displaystyle {\frac{n\mbox{sen}n}{2n^{2}-1}}$.

  31. Demuestre que (an) converge a l si, y solo si, (| an - l|) converge a 0.

  32. Si an $ \rightarrow$ l, demuestre que | an| $ \rightarrow$ | l|.

  33. Considere (an) dada recurrentemente por: a1 = $ \sqrt{2}$, an + 1 = $ \sqrt{1+\sqrt{a_{n}}}$, para n $ \geq$ 1.

    (a)
    Demuestre que esta sucesión es creciente. Sug. Observe que

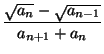    an + 1 - an = $\displaystyle {\frac{\sqrt{a_{n}}-\sqrt{a_{n-1}}}{a_{n+1}+a_{n}}}$.

    (b)
    Demuestre que $ \sqrt{2}$ $ \leq$ an $ \leq$ $ {\frac{3}{2}}$,$ \forall$ n $ \in$ IN.

    (c)
    Concluya que (an) converge a un número l que satisface l = $ \sqrt{1+\sqrt{l}}$. Calcule a1, a5, a9.

  34. Estudie la convergencia de la sucesión geométrica dada por a1 = c, an + 1 = $ \lambda$an,$ \forall$ n $ \geq$ 2.

  35. Considere la sucesión dada por a1 = 1, an + 1 = $ \sqrt{ca_{n}%% }$,$ \forall$ n $ \geq$ 2, con c > 0. Muestre que an $ \rightarrow$ c. (Sug. an2 - an - 12 = c(an - 1 - an - 2). Muestre que la sucesión es monótona y se mantiene entre c y 1).

  36. Considere la sucesión dada por x1 = 3, xn + 1 = $ {\frac{3(1+x_{n})}{3+x_{n}}}$ = 3 - $ {\frac{6}{3+a_{n}}}$,$ \forall$ n $ \geq$ 2.

    (a)
    Muestre que (an) es decreciente, y an $ \geq$ $ \sqrt{3}$,$ \forall$ n $ \in$ IN.

    (b)
    Concluya que an $ \rightarrow$ $ \sqrt{3}$.

  37. (Existencia de raíces vía sucesiones) Considere p $ \in$ IN. Dado x0 tal que x0p > a > 1, considere la sucesión definida recurrentemente por

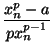    xn + 1 = xn - $\displaystyle {\frac{x_{n}^{p}-a}{px_{n}^{p-1}}}$,  $\displaystyle \forall$n $\displaystyle \in$ IN.

    (a)
    Muestre por inducción que xnp > a, para todo n $ \in$ IN. Sug. Escriba

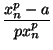
    xn + 1p = xnp$\displaystyle \left(\vphantom{ 1-\frac{x_{n}^{p}-a}{px_{n}^{p}}}\right.$1 - $\displaystyle {\frac{x_{n}^{p}-a}{px_{n}^{p}}}$$\displaystyle \left.\vphantom{ 1-\frac{x_{n}^{p}-a}{px_{n}^{p}}}\right)^{p}_{}$,

    y luego use la desigualdad de Bernoulli (ejercicio 3).

    (b)
    Use la parte anterior para mostrar que $ \left(\vphantom{ x_{n}}\right.$xn$ \left.\vphantom{ x_{n}}\right)$ es decreciente. Sug. Para el paso inductivo escriba

    xn + 1 = $\displaystyle {\frac{p-1}{p}}$xn + $\displaystyle {\frac{a}{px_{n}^{p-1}}}$,

    y recuerde que a < xnp.

    (c)
    Concluya que $ \left(\vphantom{ x_{n}}\right.$xn$ \left.\vphantom{ x_{n}}\right)$ es convergente, y que $ \alpha$ = lim xn es tal que $ \alpha^{p}_{}$ = a.

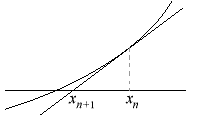
    Nota: Esta sucesión se obtiene aplicando el método de Newton a la función f (x) = xn - a. Es decir, para cada n se considera la recta tangente al gráfico de f, en el punto $ \left(\vphantom{ x_{n},f\left( x_{n}\right) }\right.$xn, f$ \left(\vphantom{ x_{n}}\right.$xn$ \left.\vphantom{ x_{n}}\right)$$ \left.\vphantom{ x_{n},f\left( x_{n}\right) }\right)$, y se define xn + 1 como el punto en que esa recta corta al eje x. En efecto, la recta tangente en el punto $ \left(\vphantom{ x_{n},f\left( x_{n}\right) }\right.$xn, f$ \left(\vphantom{ x_{n}}\right.$xn$ \left.\vphantom{ x_{n}}\right)$$ \left.\vphantom{ x_{n},f\left( x_{n}\right) }\right)$ tiene ecuación

    y = f$\scriptstyle \prime$$\displaystyle \left(\vphantom{ x_{n}}\right.$xn$\displaystyle \left.\vphantom{ x_{n}}\right)$$\displaystyle \left(\vphantom{ x-x_{n}}\right.$x - xn$\displaystyle \left.\vphantom{ x-x_{n}}\right)$ + f$\displaystyle \left(\vphantom{ x_{n}}\right.$xn$\displaystyle \left.\vphantom{ x_{n}}\right)$.

    Para encontrar el punto en que esta recta corta al eje x, debemos resolver

    f$\scriptstyle \prime$$\displaystyle \left(\vphantom{ x_{n}}\right.$xn$\displaystyle \left.\vphantom{ x_{n}}\right)$$\displaystyle \left(\vphantom{ x-x_{n}}\right.$x - xn$\displaystyle \left.\vphantom{ x-x_{n}}\right)$ + f$\displaystyle \left(\vphantom{ x_{n}}\right.$xn$\displaystyle \left.\vphantom{ x_{n}}\right)$ = 0,

    con lo cual obtenemos

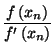    x = xn - $\displaystyle {\frac{f\left( x_{n}\right) }{f^{\prime}\left( x_{n}\right) }}$ = xn - $\displaystyle {\frac{x_{n}^{p}-a}{px_{n}^{p-1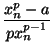}}}$ = xn + 1.

    Usted debe demostrar que $ \left(\vphantom{ x_{n}}\right.$xn$ \left.\vphantom{ x_{n}}\right)$ converge a la raíz positiva de f, lo cual es geométricamente evidente.

  Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28