|
|
| Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
En esta sección motivamos la definición del número e que daremos en la siguiente. Si el lector no está familiarizado con la noción de derivada, puede pasar directamente a la sección 4.5.
Sea
g![]() x
x![]() = logax, y tratemos de derivar esta función en
x = 1. Tenemos
= logax, y tratemos de derivar esta función en
x = 1. Tenemos
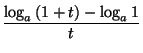 =
= Para x > 0 arbitrario tenemos
g
![]() (x)
(x)=
![]() ln x =
ln x = ![]()
![]() =
= ![]()
![]() ln
ln![]() 1 +
1 + ![]()
![]()
=
![]()
![]()
![]() ln
ln![]() 1 +
1 + ![]()
![]() =
= ![]()
![]()
![]() =
= ![]() ,
,
donde hemos hecho el cambio
u = ![]() , y usamos (4.3).
, y usamos (4.3).
Tratemos ahora de derivar la función f (x) = ex. Como f es continua, haciendo el cambio t = eh tenemos
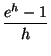 =
= 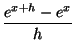 = ex
= ex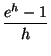 = ex,
= ex,