Sea a > 1, y consideremos la función
f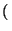 x
x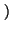 = ax
acabada de definir.
= ax
acabada de definir.
Recordemos la desigualdad (4.1):
1 <
a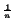
< 1 +
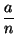
, para
a > 1 y
n 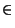 IN
IN.
Dado
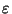 > 0, sea
n
> 0, sea
n 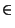 IN tal que
IN tal que
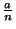 <
< 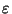 . Luego para
-
. Luego para
- 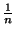 < x <
< x < 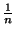 tenemos
tenemos
y también
Esto demuestra que tomando
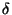 =
= 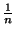 se tiene
lo que significa
se tiene
lo que significa
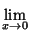 ax
ax = 1.
En otras palabras, la función exponencial es continua en x = 0. En
general, haciendo el cambio t = x - x0 tenemos:
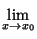 ax
ax =
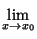 ax0 . ax - x0
ax0 . ax - x0 =
ax0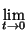 at
at =
ax0,
y entonces la función exponencial de base a es continua en todo
IR.
Ahora que tenemos la continuidad, podemos usar el teorema de valores
intermedios para concluir que el rango de la función exponencial es todo
IR+. Para esto consideremos y > 0 y observemos que
Por arquimedianidad existe
n1 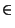 IN tal que
n1
IN tal que
n1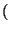 a - 1
a - 1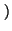 > y, de donde
> y, de donde
an1 >
n1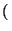 a
a - 1
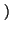
>
y.
De la misma forma existe
n0 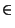 IN tal que
n0
IN tal que
n0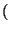 a - 1
a - 1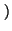 >
> 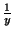 , de donde
an0 >
, de donde
an0 > 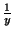 . Consecuentemente
tenemos
. Consecuentemente
tenemos
a-n0 < y < an1.
Por el teorema de los valores intermedios, existe
x 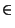
![$ \left]\vphantom{
-n_{0},n_{1}}\right.$](img609.gif) - n0, n1
- n0, n1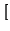 tal que ax = y. Esto demuestra que la función
tal que ax = y. Esto demuestra que la función
f : IR 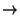 ![$\displaystyle \left]\vphantom{ 0,\infty}\right.$](img611.gif) 0, 0,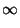 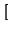 , f , f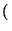 x x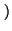 = ax, = ax, |
(4.2) |
es sobreyectiva.
Como ya sabíamos que
era inyectiva (por ser estrictamente creciente), se concluye que es de hecho
biyectiva.
Nota: Para 0 < a < 1 tenemos
ax =
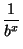
, con
b =
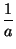
> 1,
y no es difícil convencerse de que sigue siendo biyectiva y continua. En
adelante, cuando hablemos de la función exponencial, nos referimos a la
función deinida por (4.2), con a > 0 y a 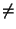 1. Resumamos lo
que tenemos:
1. Resumamos lo
que tenemos:
Teorema 7
La función exponencial dada en (
4.2) es biyectiva y continua.
Además, es estrictamente creciente si
a > 1, y estrictamente decreciente
se 0 <
a < 1.
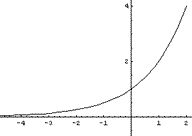
El gráfico de f tiene la siguiente representación geométrica, en
el caso a > 1 :
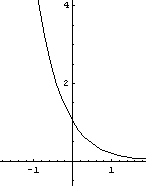
En el caso 0 < a < 1 la función resulta decreciente, y su gráfico se
representa así:
![]() x
x![]() = ax
acabada de definir.
= ax
acabada de definir.
![]() > 0, sea
n
> 0, sea
n ![]() IN tal que
IN tal que
![]() <
< ![]() . Luego para
-
. Luego para
- ![]() < x <
< x < ![]() tenemos
tenemos
![]()
![]() - n0, n1
- n0, n1![]() tal que ax = y. Esto demuestra que la función
tal que ax = y. Esto demuestra que la función

