|
|
| Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
Una manera de iniciar el estudio de los números naturales es comenzar con los axiomas de Peano, que incluyen el principio de inducción. Si se está familiarizado con los números reales, se puede definir el conjunto IN de los números naturales como el menor subconjunto inductivo de IR. Aquí nos contentaremos con enunciar el principio de inducción como axioma.
![]() A.
A.
![]() A se tiene n + 1
A se tiene n + 1 ![]() A.
A.
Por ejemplo,
A = [0,![]() [ es inductivo, lo mismo que IN y
IZ. El conjunto
[ es inductivo, lo mismo que IN y
IZ. El conjunto
Principio de inducción (Versión 1)
IN es el menor
subconjunto inductivo de IR.
Así, si
A ![]() IN es inductivo, debe tenerse
A = IN.
Podemos entonces escribir el principio en la forma alternativa:
IN es inductivo, debe tenerse
A = IN.
Podemos entonces escribir el principio en la forma alternativa:
Principio de inducción (Versión 2) Si
A ![]() IN
satisface la propiedades (a) y (b), entonces A = IN.
IN
satisface la propiedades (a) y (b), entonces A = IN.
Definimos el conjunto
Ahora, si n ![]() A tenemos
2n
A tenemos
2n ![]() n + 1. Entonces
n + 1. Entonces
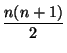 .
.
Se trata de demostrar que el conjunto
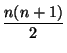
Para n = 0, la suma del lado izquierdo solo tiene un término, y es igual a
0, mientras que el lado derecho es
![]() = 0. Entonces 0
= 0. Entonces 0 ![]() A.
A.
Si n ![]() A, entonces tenemos que
A, entonces tenemos que
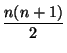 ,
,
![$\displaystyle \begin{array}[c]{ccc}%%
0+1+\cdots+(n+1) & = & \left( 0+\cdots+n\...
...& \frac{n(n+1)+2(n+1)}{2}\smallskip\\
& = & \frac{(n+1)(n+2)}{2},
\end{array}$](img51.gif)
Nota: En la práctica no se scodtumbra definir el conjunto A explícitamente, sino que se demuestra la propiedad planteada para n = 0, y luego se demuestra que si se cumple para n, debe cumplirse para n + 1.
En efecto, para n = 0 tenemos n3 + 5n = 0, el cual es divisible por 6.
Si n3 + 5n es divisible por 6, tenemos
n3 + 5n = 6k, para algún
k ![]() IN. Luego
IN. Luego
Como
n![]() n + 1
n + 1![]() es siempre par (¿por qué?),
tenemos que
3n
es siempre par (¿por qué?),
tenemos que
3n![]() n + 1
n + 1![]() es múltiplo de 6, y
consecuentemente
es múltiplo de 6, y
consecuentemente
![]() n + 1
n + 1![]() + 5
+ 5![]() n + 1
n + 1![]() lo es.
lo es.
El principio de inducción también es aplicable a propiedades que son válidas a partir de cierto valor de n. Veamos el siguiente resultado, que llamaremos inducción truncada.
(a) N ![]() A.
A.
(b) Para todo n ![]() A tal que n
A tal que n ![]() N, se tiene
n + 1
N, se tiene
n + 1 ![]() A.
A.
Entonces A contiene todos los naturales a partir de N. Esto es:
Prueba:
Si N = 0, el resultado es precisamente el principio de inducción.
Si N > 0 considere el conjunto
Veamos algunos ejemplos donde se aplica este resultado:
Note que en este caso la desigualdad es falsa para n = 0, 1, 2. Para n = 3
sí es válida pues tenemos
3 + 3 = 6 < 23 = 8. Ahora, si se cumple para
cierto n ![]() 3, tenemos
n + 3 < 2n, y luego
3, tenemos
n + 3 < 2n, y luego
Note que aunque la desigualdad es válida para n = 1 y n = 2, no lo es para
n = 3. Para n = 4 tenemos
42 = 16 = 24, así que se cumple
42 ![]() 24.
24.
Ahora supongamos que se cumple para algún n ![]() 4, esto es
n2
4, esto es
n2 ![]() 2n. Entonces
2n. Entonces
En algunos ejemplos, al demostrar que n + 1 ![]() A, se debe hacer uso no solo
del hecho que n
A, se debe hacer uso no solo
del hecho que n ![]() A, sino también de que n - 1
A, sino también de que n - 1 ![]() A, o en general de
que k
A, o en general de
que k ![]() A para k
A para k ![]() n. El siguiente resultado permite hacer este tipo de razonamientos.
n. El siguiente resultado permite hacer este tipo de razonamientos.
Entonces A = IN.
Prueba
Defina el conjunto
Otra propiedad importante de los números naturales es el principio del
buen orden
. Como veremos, este principio es equivalente
al principio de inducción. Para establecerlo necesitamos primero la
siguiente definición.
El lector puede demostrar que de existir el primer elemento, este debe ser
único. Note que 0 es el primer elemento de IN. Dado
A ![]() IN, si 0
IN, si 0 ![]() A se sigue inmediatamente que 0 es el
primer elemento de A.
A se sigue inmediatamente que 0 es el
primer elemento de A.
Prueba
Suponga que A no tiene primer elemento, y defina
Por el principio de inducción completa se sigue que
B = IN, y
consecuentemente
A = ![]() . Como esto contradice la hipótesis, A
debe tener primer elemento.
. Como esto contradice la hipótesis, A
debe tener primer elemento.
Como una aplicación de este hecho, demostremos que todo número real tiene parte entera.
Si x < 0, se aplica lo anterior a - x y luego se multiplica por -1.
Nota: El lector puede convencerse de que m es único para x.
Tal m se llama la parte entera de x, y se denota
m = ![]() x
x![]() .
.
La idea es comenzar en el origen, ``pegando brincos'' de longitud b, hasta
caer a la derecha de a. Entonces q es el mayor natural que cumple qb ![]() a. Basta entonces con tomar
q =
a. Basta entonces con tomar
q = ![]()
![]()
![]() . Tenemos
. Tenemos
Visto de otra forma, q = k0 - 1, donde k0 es el primer elemento del conjunto
Por ejemplo, si a = 145 y b = 15, tenemos a = b . 9 + 10, así que q = 9 y r = 10.
Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28