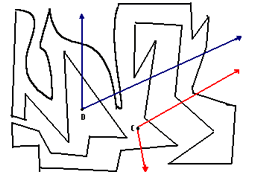
El teorema de la curva de Jordan Brawer

Este teorema es un resultado cuya demostración es bastante elaborada y necesita de un alto nivel de matemática para su formalización. Sin embargo, intuitivamente dice algo bastante sencillo. El esencia, el teorema de la curva cerrada de Jordan Brower indica que cualquier curva cerrada simple separa el plano en tres regiones disjuntas: el exterior, el interior y la curva misma.

(Teorema de la curva de jordan) Sea una curva cerrada simple en el plano.⁶ . Entonces separa al plano en exactamente dos componentes y . Cada uno de los conjuntos y tiene a como su frontera.

Este teorema es intuitivamente evidente si la curva es simple muy simple como es el caso de un círculo. Pero si la curva fuese considerablemente más compleja, el resultado no sería tan evidente a simple vista.

Lo interesante es este caso y que es de utilidad en un contexto de primaria y secundaria son los resultados que llevan a la demostración del teorema. La demostración usa el hecho de que un punto cualquiera estará ``adentro'' de la curva si al trazar un rayo con origen en en cualquier dirección y de forma que el rayo corte a la curva de forma transversal <sup>7</sup> en todo punto de intersección, entonces el número de cortes será un número impar. De lo contrario, esto es, si el punto se encuentra ``afuera de la curva, entonces cualquier yayo con origen en que corte transversalmente a la curva lo hará un número par de veces. En el dibujo podemos apreciar como el punto se encuentra dentro de la curva y no importa en la dirección que tracemos un rayo transversal, este cortara la curva un número impar de veces. Por otro lado, el punto esta fuera de la curva y cualquier rayo trazado desde el que corte la curva transversalmente, lo hará un número par de veces.