|
Inicio 1 2
3 4 5
6 7 8
9 10
11
12 13 14
La Fórmula de Euler para poliedros
Este es un resultado muy interesante y visualmente sorprendente.
Considere un poliedro P no importa si este es regular o
irregular. La fórmula de Euler indica que si 
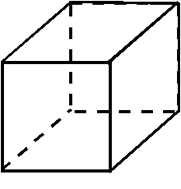
Por ejemplo si tomamos un cubo cualquiera este tendrá seis caras, ocho vértices y doce aristas. En este caso
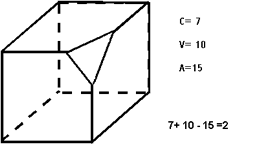
Ahora bien, si hacemos un corte en una esquina obtenemos un nuevo poliedro irregular que guarda la misma relación entre sus caras, aristas y vértices
De hecho no importa cuantos cortes se le apliquen y lo irregular de la forma final la igualdad anterior seguirá siendo válida. Este tipo de resultado puede ser útil para mejorar la capacidad visual, la motora fina y los procesos aritméticos en los estudiantes de los primeros niveles usando como estrategia didáctica la construcción y posterior corte de un poliedro, para que el estudiante verifique con algunos ejemplos la validez de la fórmula.
|
representa el
número de caras del poliedro, 
representa el número de
aristas y 
representa el número de vértices del poliedro
entonces se cumple que
de donde fácilmente vemos que
