El Teorema de Morley

Descubierto hacia 1899 por Frank Morley, profesor de matemáticas de la Universidad John Hopkins, el teorema que lleva su nombre es un resultado que sorprendió a la comunidad matemática por cuanto es un resultado de la geometría clásica que no fue descubierto por los griegos⁵. Se cuenta que debido a esto, Morley vivía descontento por haber encontrado este resultado dado que el interés de los matemáticos se centró en él y no en la obra completa desarrollada por Morley.

El enunciado original no parece ser nada intuitivamente interesante y dice lo siguiente:

Si una cardioide variable sea tangente a los lados de un triángulo, entonces el lugar geométrico de su centro, esto es, del centro del círculo sobre el cual rodan las circunferencias iguales, es un conjunto de 9 rectas que son paralelos a las direcciones siendo ellas de un triángulo equilátero. Las intersecciones de estas rectas corresponden a las tangentes dobles y también son las intersecciones de pares de trisectrices de los ángulos internos y externos del primer triángulo.

Este enunciado se encontraba en un trabajos sobre cardioides elaborado por Morley .

"Para ver una demostración se puede consultar: "Introduction to Geometry" de Coxeter, editado por "John Wiley & Sons, Inc". "(Fleitas,[12]).

Un enunciado reducido de este teorema y que muestra lo interesante del resultado dice:

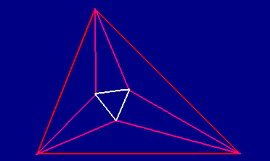
(Teorema de Morley) Los pares adyacentes de las trisectrices de los ángulos de un triángulo siempre se encuentran en los vértices de un triángulo equilátero.

El profesor podrá emplear este resultado para que el estudiante práctique construcciones geométricas, desarrolle habilidad en el uso de los instrumentos geométricos, y mejore motora fina.