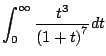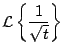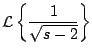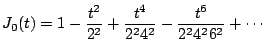|
Función Gamma
Ahora estudiaremos una función conocida como la función gamma 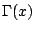 , la cual es de gran importacia en análisis y en aplicaciones. Esta función se define en términos de una integral impropia, la cual no puede calcularse en términos de funciones elementales. , la cual es de gran importacia en análisis y en aplicaciones. Esta función se define en términos de una integral impropia, la cual no puede calcularse en términos de funciones elementales.
|
|
Definición
[Función Gamma]
|
| |
La función
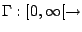 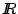  dada por dada por
|
se conoce como la función gamma. Su gráfica se muestra en la figura
1.9.
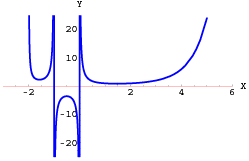
Figura 1.9
El siguiente teorema establece una de las propiedades más importantes de la función gamma.
|
|
Teorema
[Recursividad de gamma]
|
| |
Para toda 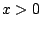 se tiene que se tiene que
|
Demostración
Integrando por partes
Ejemplo
Calcule
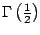 . .
Solución
El resultado anterior puede generalizarse, como muestra en el siguiente corolario.
|
|
Corolario
[Recursividad de Gamma]
|
| |
Para 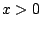 , ,
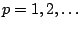 y y
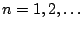 se tiene que se tiene que
|
Observación: de los resultados anteriores obtenemos que
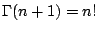 , por esta razón se conoce a esta función como el factorial generalizado. , por esta razón se conoce a esta función como el factorial generalizado.
Ejemplo
Calcular los valores de
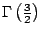 , ,
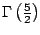 , ,
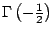 . .
Solución
Usando la propiedad recursiva, tenemos que
- Para
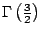 : :
- Para
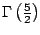 : :
- Para
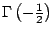 : :
De donde
|
|
Definición
[Función Beta]
|
| |
La siguiente integral
se conoce como la función beta.
|
El siguiente teorema enuncia algunas de las propiedades de la función Beta.
|
|
Teorema
[Propiedades de la función beta]
|
| |
- La función
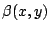 converge para converge para 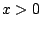 , , 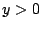 . .
-
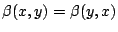 . .
- Para
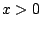 , , 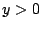 se tiene que se tiene que
- Para
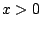 , , 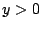 se tiene que se tiene que
- Para
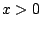 , , 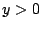 se tiene que se tiene que
|
Demostración
- Para demostrar que la integral convege, separemos la integral en dos partes
Ahora, observe que la primera integral convwerge si
y de igual manera, la segunda integral converge si
- Para demostrar esta propiedad basta hacer un cambio de variable
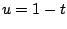
- Haciendo el cambio de variable
tenemos que
- Haciendo el cambio de variable
tenemos que
- La demostración de este resultado es un tanto más compleja y se sale de los objetivos del curso, por esta razón no la haremos.
Ejemplo
Calcule el valor de la siguiente integral
Solución
Usando los resultados del teorema anterior
Observe que cuando 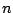 es muy grande es extremadamente difícil calcular es muy grande es extremadamente difícil calcular 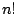 , aún con la ayuda de logaritmos. Por ejemplo, la tarea de determinar el número de posibles formas de barajar un maso de cartas podría tomar mucho tiempo, pues involucra el calculo de , aún con la ayuda de logaritmos. Por ejemplo, la tarea de determinar el número de posibles formas de barajar un maso de cartas podría tomar mucho tiempo, pues involucra el calculo de 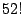 . El siguiente teorema establece que . El siguiente teorema establece que
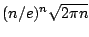 es una buena aproximación de es una buena aproximación de 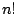 , cuando , cuando 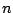 es muy grande. es muy grande.
|
|
Teorema
[Fórmula de Stirling]
|
| |
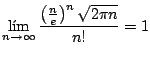
|
Observación: del la fórmula de Stirling1.4 tenemos que
Y por último el siguiente teorema expresa la relación entre la función 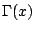 y la transformada. y la transformada.
|
|
Teorema
[Transformada de 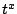 ] ]
|
| |
Para 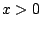 , tenemos que , tenemos que
|
Demostración
Usando la definición de transformada y la sustitución 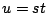 , tenemos que , tenemos que
Ejemplo
Calcule
Solución
Usando el teorema anterior
Ejemplo
Calcule
Solución
Usando el primer teorema de traslación, tenemos que
Ejemplo
Calcule
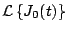 donde donde  es la función de Bessel de orden cero dada por la serie es la función de Bessel de orden cero dada por la serie
Solución
Aplicando transformada de Laplace
Observación: en este ejemplo hemos usado que
para
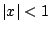 . .
Revista digital Matemática, Educación e Internet.
|