|
|
|
|
|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M. |
1 2 3
4 5
6 7
8 9
10 11
12 13
14 15
16
|
|
Propiedades de la Transformada de Laplace Como la transformada de Laplace se define en términos de una integral impropia que puede ser divergente, existen funciones para las cuales no existe dicha transformada, incluso hay funciones discontinuas, como la del ejemplo anterior, que pueden tener transformada; entonces, ¿ bajo qué condiciones una funciones tienen transformada de Laplace ?. Antes de dar una respuesta parcial a esta pregunta debemos dar algunas definiciones.
En general, el requisito de que estos límites sean finitos en todos los
puntos
Figura 1.2
Intuitivamente podríamos pensar que las funciones continuas a trozos son casi continua o que no son demasiado discontinua. Otra de las ideas importantes en el estudio de la existencia de la transformada de Laplace es que entendemos porqué una función no crezca demasiado rápido.
Intuitivamente esto significa que la función
Figura 1.3
Observación: algunas veces, para verificar que una función
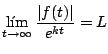
para algún valor de
Ejemplo
Solución
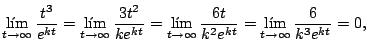
para cualquier número positivo
Ejemplo
Solución
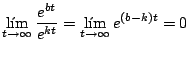
siempre y cuando
Observación: no es difícil comprobar que cualquier polinomio de grado
Ejemplo
Solución
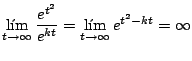
para cualquier valor de El siguiente resultado enuncia un resultado que parece obvio.
Demostración
Como
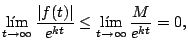
para cualquier
Observación: como Una vez definidos los conceptos de función continua a trozos y función de orden exponencial ya estamos listos para enunciar una condición necesaria para la existencia de la transformada de Laplace.
Demostración
Por ser
La primera integral
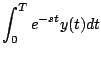
es una integral definida, por tanto existe. Para la segunda integral note que
Ahora, como
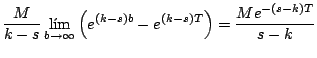
siempre y cuando
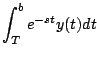
existe y con ello la transformada.
Observación: el teorema anterior enuncia una condición suficiente y no
necesaria para la existencia de la transformada de Laplace, es decir, puede
darse el caso de una función
Ejemplo
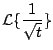
existe, aún cuando
Solución
Para calcular esta última integral sea
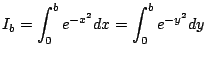
con lo cual
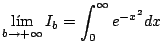
Ahora note que
Figura 1.4
Donde
Con lo cual, tomando el límite
Y así,
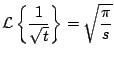
El siguiente ejemplo muestra una función para la cual no existe la transformada de Laplace.
Ejemplo
no existe.
Solución
Y puesto que la integral impropia
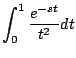
diverge, la transformada no existe. Observación: la otra integral
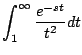
es convergente para
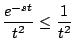
La integral
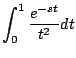
diverge, pues, por el criterio de comparación
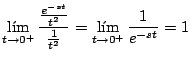
para toda
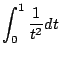
diverge. Ahora vamos a enunciar algunos propiedades de la transformada.
Demostración
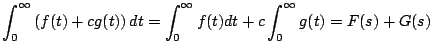
Ejemplo
Solución
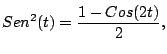
por la propiedad de linealidad
Con la idea de aplicar la transformada de Laplace a la solución de ecuaciones diferenciales necesitamos calcular la transformada de una derivada.
Demostración
Integrando por partes
Con un argumento similar podemos demostrar que
Ejemplo
Solución
y de aquí concluimos que
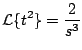
El siguiente resultado generaliza la transformada de una derivada.
El siguiente teorema trata sobre el efecto que tiene en una transformada la
escalación de una función
Demostración
Ejemplo
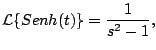
calcule
Solución Usando la propiedad de escalamiento
|