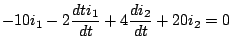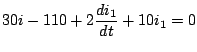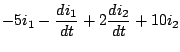|Instituto Tecnológico de Costa Rica|Escuela de Matemática|  M. Sc. Geovanni Figueroa M.


1 2  3  4  5  6  7  8  9  10  11  12  13  14  15  16

 

 

 

  

Sistemas de ecuaciones diferenciales

El siguiente ejemplo muestra el uso de la transformada de Laplace en la solución de sistemas de ecuaciones diferenciales.

Ejemplo
Resuelva el siguiente sistema de ecuaciones diferenciales


$\displaystyle \frac{dx}{dt}$ $\displaystyle =$ $\displaystyle 2x - 3y$
$\displaystyle \frac{dy}{dt}$ $\displaystyle =$ $\displaystyle y - 2x$

con las condiciones $ x(0)=8$, $ y(0)=3$.

Solución
Si $ {\cal L} \{ x(t) \}=X(s)$ y $ {\cal L} \{y(t) \} = Y(s)$, entonces


$\displaystyle sX(s) - 8$ $\displaystyle =$ $\displaystyle 2X(s) - 3Y(s)$
$\displaystyle sY(s) - 3$ $\displaystyle =$ $\displaystyle Y(s) - 2X(s)$

o agrupando


$\displaystyle \left(s - 2 \right)X(s) + 3Y(s)$ $\displaystyle =$ $\displaystyle 8$
$\displaystyle 2X(s) + \left(s - 1 \right)Y(s)$ $\displaystyle =$ $\displaystyle 3$

Ahora usemos la regla de Cramer para resolver el sistema anterior

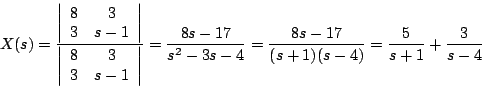
\begin{displaymath} X(s) = \frac{\biggr\vert \begin{array}{cc} 8 & 3 \\ 3 & s-... ...4} = \frac{8s-17}{(s+1)(s-4)} = \frac{5}{s+1} + \frac{3}{s-4} \end{displaymath}

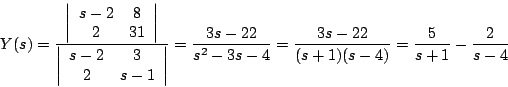
\begin{displaymath} Y(s) = \frac{\biggr\vert \begin{array}{cc} s-2 & 8 \\ 2 & ... ...4} = \frac{3s-22}{(s+1)(s-4)} = \frac{5}{s+1} - \frac{2}{s-4} \end{displaymath}

De donde obtenemos que

$\displaystyle x(t) = {\cal L}^{-1} \{X(s) \} = 5e^{-t} + 3e^{4t} $

$\displaystyle y(t) = {\cal L} \{Y(s) \} = 5e^{-t} - 2e^{4t} $

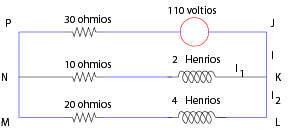
Ejemplo
Dada la malla eléctrica de la figura 1.15, determine el valor de las corrientes $ i_1$ y $ i_2$, si inicialmente valen cero.

Figura 1.15

Solución
Puesto que la segunda ley de Kirchhoff establece que la suma algebraica de las caídas de voltaje alrededor de cualquier malla cerrada es cero, tenemos que:

  • Para la malla KLMNK

    $\displaystyle -10i_1 - 2 \frac{dti_1}{dt} + 4 \frac{di_2}{dt} + 20 i_2 = 0 $

  • Y para la malla JKNPJ:

    $\displaystyle 30 i - 110 + 2 \frac{di_1}{dt} + 10 i_1 = 0 $

De donde obtenemos el siguiente sistema:


$\displaystyle -5i_1 - \frac{di_1}{dt} + 2 \frac{di_2}{dt} + 10i_2$ $\displaystyle =$ 0
$\displaystyle \frac{di_1}{dt} + 20 i_1 + 15i_2$ $\displaystyle =$ $\displaystyle 55$

Tomando transformada de Laplace y usando las condiciones iniciales, $ i_1(0)=i_2(0)=0$, obtenemos que


$\displaystyle \left( s + 5 \right)i_1 - \left(2s + 10 \right)i_2$ $\displaystyle =$ 0
$\displaystyle \left( s + 20 \right)i_1 + 15i_2$ $\displaystyle =$ $\displaystyle \frac{55}{s}$

Observe que de la primera ecuación $ i_1=2i_2$, de modo que la segunda ecuación se transforma en

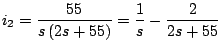
$\displaystyle i_2 = \frac{55}{s \left(2s + 55 \right)} = \frac{1}{s} - \frac{2}{2s+55} $

Entonces

$\displaystyle i_2(t) = 1 - e^{-\frac{55t}{2}} $

$\displaystyle i_1(t) = 2i_2 = 2 - 2 e^{-\frac{55t}{2}} $

y

$\displaystyle i(t) = i_1(t) + i_2(t) = 3 \left(1 - e^{-\frac{55t}{2}} \right) $

 

 

 

 

Inicio Revista digital Matemática, Educación e Internet.