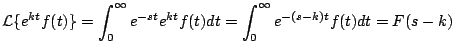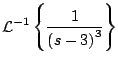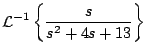|
Teoremas de traslación
No es adecuado utilizar la definición cada vez que se quiera calcular una transformada, por ejemplo, la integración por partes involucrada al calcular
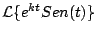 , es bastante tediosa. Por esta razón vamos a enunciar algunos teoremas que ahorran trabajo en el cálculo de este tipo de transformadas. , es bastante tediosa. Por esta razón vamos a enunciar algunos teoremas que ahorran trabajo en el cálculo de este tipo de transformadas.
Si conocemos que
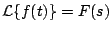 , podemos calcular la transformada de , podemos calcular la transformada de
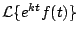 como una traslación, de como una traslación, de 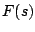 a a 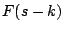 , como lo enuncia el siguiente teorema. , como lo enuncia el siguiente teorema.
|
|
Teorema
[Primer teorema de traslación]
|
| |
Si 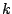 es un número real y es un número real y
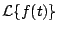 existe, entonces existe, entonces
donde
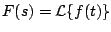 . .
Forma inversa del primer teorema de traslación:
|
Demostración
La prueba es inmediata apartir de la definción
Observación: si consideramos a 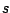 como una variable real, entonces la gráfica de como una variable real, entonces la gráfica de 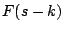 es la misma de es la misma de 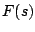 trasladada trasladada 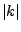 unidades sobre el eje unidades sobre el eje 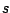 . Si . Si 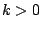 , la gráfica de , la gráfica de 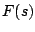 se desplaza se desplaza 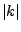 unidades a la derecha, miéntras que, si unidades a la derecha, miéntras que, si 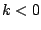 , la gráfica se traslada , la gráfica se traslada 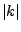 unidades a la izquierda. Para enfatizar en la traslación se acostumbra escribir unidades a la izquierda. Para enfatizar en la traslación se acostumbra escribir
donde
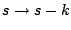 significa que se sustituye significa que se sustituye 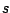 por por 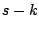 en en 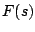 . .
Ejemplo
Calcule
Solución
Usando el primer teorema de traslación
Ejemplo
Use la forma inversa del primer teorema de traslación para calcular
Solución
Ejemplo
Calcule
Solución
Para usar la forma inversa del primer teorema de traslación debemos completar el cuadrado en el denominador
Subsecciones
Revista digital Matemática, Educación e Internet.
|