|Instituto Tecnológico de Costa Rica|Escuela de Matemática|  M. Sc. Geovanni Figueroa M.

1 2  3  4  5  6  7  8  9  10  11  12  13  14  15  16

 

 

 

 

Convolución y transformadas

Como hemos visto, la transformada de Laplace es lineal, es decir, la transformada de una suma es la suma de las transformadas, entonces cabe preguntarse si se tiene algo similar para el producto, la respuesta es no. En general la transformada no conmuta con la multiplicación ordinaria, o sea, la transformada de un producto no es el producto de las transformadas, pero podemos definir un nuevo producto generalizado bajo el cual esto es cierto.

 

	Definición [Convolución]
	La función $h: {\cal C}(I) \times {\cal C}(I) \rightarrow {\cal C}(I)$, donde ${\cal C}$ es el conjunto de funciones continuas en el intervalo $I=[0, +\infty[$ dada por $$h(t)= \left(f \star g \right)(t) = \int_0^t f(t - \tau ) g(\tau ) d \tau$$ se conoce como la convolución de $f$ y $g$.

 

La convolución tiene muchas de las propiedades de la multiplicación ordinaria, como veremos en el siguiente teorema.

 

	Teorema [Propiedades de la convolución]
	Sean $f$ y $g$ funciones continuas en el intervalo $[0,+ \infty[$, entonces $f \star g = g \star f$ (ley conmutativa) $f \star ( g + h ) = f \star g + f \star h$ (ley distributiva) $(f \star g) \star h = f \star (g \star h)$ (ley asociativa) $f \star 0 = 0 \star f = 0$

Demostración

La demostración de estas propiedades es muy simple. Haremos la primera de ellas y dejamos las restantes al lector.

$$(f \star g)(t) = \int_0^t f(\tau) g(\underbrace{t - \tau}_{u=t - \tau}) d \tau$$

$$= - \int_t^0 f(t-u) g(u) du$$

$$= \int_0^t g(u) f(t-u) du$$

$$= (g \star f)(t)$$

 

Observación: sin embargo, existen algunas propiedades de la multiplicación ordinaria que la convolución no tiene. Por ejemplo, no es cierto en general que $f \star 1 = f$; para ver esto, note que

$$Cos(t) \star 1 = \int_0^t Cos(\tau) d \tau$$

$$= Sen(\tau) \biggr\vert _0^t$$

$$= Sen(t)$$

Ejemplo
Calcule la convolución de $f(t)=e^t$ y $g(t)=Sen(t)$.

Solución
Usando la definición e integración por partes, tenemos que

$$e^t \star Sen(t) = \int_0^t e^{\tau} Sen(t- \tau) d \tau$$

$$= \frac{e^{} \left(Cos(\tau - t) - Sen(\tau - t) \right)}{2} \biggr\vert _0^t$$

$$= \frac{e^t -Sen(t) - Cos(t)}{2}$$

Ejemplo
Calcule la convolución de las funciones $f(t)=Sen(at)$ y $g(t)=Cos(bt)$.

Solución
Usando la definición e integración por partes

$$\left( Sen(at) \star Cos(bt) \right)(t) = \int_0^t Sen \left(a(t - \tau)\right) Cos(b \tau) d\tau$$

$$= \frac{1}{2} \int_0^t \left( Sen\left(at + \left( b - a\right) \tau \right) + Sen\left(at - \left(b - a \right) \tau \right) \right) d\tau$$

$$= \frac{a \left(Cos(bt) - Cos(at) \right)}{\left(a + b \right) \left(a-b \right)}$$

Observación: para calcular la integral

$$\int_0^t Sen(t - \tau) Cos(b \tau) d\tau$$

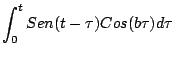
del ejemplo anterior, hemos usado la identidad

$$Sen(\alpha) Cos(\beta) = \frac{Sen(\alpha + \beta) + Sen(\alpha - \beta)}{2}$$

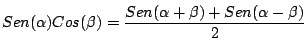
Otras identidades que pueden ser útiles en el cálculo de integrales similares son

$$Cos(\alpha) Cos(\beta) = \frac{Cos(\alpha + \beta) + Cos(\alpha - \beta)}{2}$$

$$Sen(\alpha) Sen(\beta) = \frac{Cos(\alpha - \beta) - Cos(\alpha + \beta)}{2}$$

El siguiente teorema establece un resultado de mucha importancia teórica y práctica, como veremos.

 

	Teorema [Teorema de convolución]
	Si ${\cal L} \{ f(t) \}$ y ${\cal L} \{g(t) \}$ existen para $s > a \geq 0$, entonces $${\cal L} \{(f \star g)(t) \} = {\cal L} \{f(t) \} {\cal L} \{g(t) \} = F(s) G(s)$$

Observación: La forma inversa del teorema de convolución

$$(f \star g)(t) = {\cal L}^{-1} \left(F(s) G(s) \right)$$

es muy importante en la solución de ecuaciones diferenciales, pues nos puede evitar el cálculo de fraciones parciales complejas.

Ejemplo
Calcule

$${\cal L} \{ e^t \star Sen(t) \}$$

Solución
Usando el teorema de convolución tenemos que

$${\cal L} \{ e^t \star Sen(t) \} = {\cal L} \{ e^t \} {\cal L} \{ Sen(t)\}$$

$$= \frac{1}{s-1} \frac{1}{s^2 +1}$$

$$= \frac{1}{(s+1)(s^2+1)}$$

Observación: como ya hemos calculado $e^t \star Sen(t)$ podemos corroborar el resultado obtenido anteriormente

$${\cal L} \{ e^t \star Sen(t) \} = {\cal L} \left\{ \frac{e^t -Sen(t) - Cos(t)}{2} \right\}$$

$$= \frac{1}{2} {\cal L} \{e^t \} - \frac{1}{2} {\cal L} \{ Sen(t) \} - \frac{1}{2} {\cal L} \{ Cos(t) \}$$

$$= \frac{1}{2} \left( \frac{1}{s-1} - \frac{1}{s^2+1} - \frac{s}{s^2+1} \right)$$

$$= \frac{1}{(s-1)(s^2+1)}$$

como obtuvimos en el ejemplo anterior.

Los siguientes ejemplos muestran el uso de la forma inversa del teorema de convolución para el cálculo de transformadas inversas.

Ejemplo
Calcule la siguiente transformada inversa

$${\cal L}^{-1} \left\{ \frac{1}{(s-2)(s-3)} \right\}$$

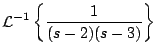
Solución
Usando el teorema de convolución

$${\cal L}^{-1} \left\{ \frac{1}{(s-2)(s-3)} \right\} = {\cal L}^{-1} \left\{ \frac{1}{s-2} \frac{1}{s-3} \right\}$$

$$= {\cal L}^{-1} \left\{ \frac{1}{s-2} \right\} \star {\cal L}^{-1} \left\{ \frac{1}{s-3} \right\}$$

$$= {\cal L} e^{2t} \star e^{3t}$$

$$= \int_0^t e^{2 \tau} e^{3(t - \tau)} d \tau$$

$$= e^{3t} - e^{2t}$$

Observación: en este ejemplo el uso de fraciones parciales resulta viable, pues

$${\cal L}^{-1} \left\{ \frac{1}{(s-2)(s-3)} \right\} = {\cal L}^{-1} \left\{ \frac{1}{s-3} - \frac{1}{s-2} \right\}$$

$$= {\cal L}^{-1} \left\{ \frac{1}{s-3} \right\} - {\cal L} \left\{ \frac{1}{s-2} \right\}$$

$$= e^{3t} - e^{2t}$$

Los siguientes ejemplos muestran situaciones donde el uso de fraciones parciales puede ser realmente complejo, comparado con el uso del teorema de convolución.

Ejemplo
Calcule la siguiente transformada inversa

$${\cal L}^{-1} \left\{ \frac{s}{(s^2 + 4)(s^2 + 9)} \right\}$$

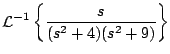
Solución
Usando el teorema de convolución, tenemos

$${\cal L}^{-1} \left\{ \frac{s}{(s^2 + 4)(s^2 + 9)} \right\} = {\cal L}^{-1} \left\{ \frac{s}{s^2 + 4} \frac{1}{s^2 + 9} \right\}$$

$$= {\cal L}^{-1} \left\{ \frac{s}{s^2+4} \right\} \star {\cal L}^{-1} \left\{ \frac{1}{s^2+9} \right\}$$

$$= Cos(2t) \star Sen(3t)$$

$$= \int_0^t Cos(2 \tau) Sen \left(3 \left(t - \tau \right) \right) d \tau$$

$$= \frac{3Cos(2t) - 3 Cos(3t) }{5}$$

Observación: en este ejemplo la expansión en fraciones parciales no es tan simple

$$\frac{1}{(s^2+4)(s^2+9)} = \frac{1}{5} \left( \frac{s}{s^2 + 4} - \frac{s}{s^2 + 9} \right)$$

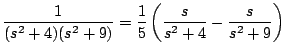
Ejemplo
Calcule la siguiente transformada inversa

$${\cal L}^{-1} \left\{ \frac{s}{(s-2)(s^2-4s+13)} \right\}$$

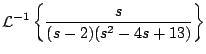
Solución
Usando convolución

$${\cal L}^{-1} \left\{ \frac{s}{(s-1)(s^2-4s+13)} \right\} = {\cal L}^{-1} \left\{ \frac{s - 2 + 2}{\left( \left( s -2 \right)^2 + 4 \right)\left(s - 1 \right)} \right\}$$

$$= {\cal L}^{-1} \left\{ \frac{s-2}{\left( \left( s -2 \right)^2 + 4 \right) \left(s - 1 \right)} \right\}$$

$$+ {\cal L}^{-1} \left\{ \frac{2}{\left( \left( s -2 \right)^2 + 4 \right) \left(s - 1 \right)} \right\}$$

$$= e^{2t}Cos(3t) \star e^{t} + e^{2t} Sen(3t) \star e^{t}$$

$$= \frac{e^t \left(1 - e^t Cos(3t) + 2e^t Sen(3t) \right)}{5}$$

El siguiente corolario es útil en el cálculo de la transformada de una integral.

 

	Corolario
	Tomando $g(t)=1$ en el teorema de convolución tenemos que $$\frac{F(s)}{s} = {\cal L} \left\{ \int_0^t f(\tau) d \tau \right\}$$ donde $F(s) = {\cal L} \{ f(t) \}$

Demostración

$${\cal L} \{ f \star 1 \} = {\cal L} \{f(t) \} {\cal L} \{ 1 \}$$

$${\cal L} \{ \int_0^t f(\tau) d\tau \} = \frac{F(s)}{s}$$

 

Ejemplo
Calcule la siguiente transformada

$${\cal L} \left\{ \int_0^t \tau Sen(\tau) d\tau \right\}$$

Solución
Usando el corolario anterior y el teorema de multiplicación por $t^n$, tenemos que

$${\cal L} \left\{ \int_0^t \tau Sen(\tau) d\tau \right\} = \frac{{\cal L} \left\{ t Sen(t) \right\} }{s}$$

$$= - \frac{ \left( {\cal L} \{ Sen(t) \} \right)^{\prime}}{s}$$

$$= -\frac{1}{s} \left( \frac{s}{s^2+1} \right)^{\prime}$$

$$= \frac{s^2 - 1}{s \left( s^2 + 1 \right)^2}$$

 

 

Revista digital Matemática, Educación e Internet.