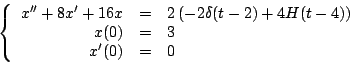|
Sistemas mecánicos
Ejemplo
Un peso de 16 libras suspendido de un resorte lo estira 2 pies. En el instante 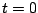 el peso se hala 3 pies por debajo de la posición de equilibrio y se suelta. Asuma una fuerza amortiguadora de 4 veces la velocidad instantánea. En el instánte el peso se hala 3 pies por debajo de la posición de equilibrio y se suelta. Asuma una fuerza amortiguadora de 4 veces la velocidad instantánea. En el instánte 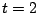 el peso recibe un golpe seco, desde abajo, que transmite 2 unidades de momentum a la masa; además, en el instante el peso recibe un golpe seco, desde abajo, que transmite 2 unidades de momentum a la masa; además, en el instante 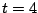 se activa una fuerza externa con una magnitud de 4 unidades. Entonces se activa una fuerza externa con una magnitud de 4 unidades. Entonces
- Determine la ecuación diferencial y condiciones iniciales que describen el movimiento.
- Encuentre la posición del peso en cualquier instante
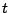 . .
- ¿Cuál es la posición del peso en
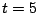 ? ?
Solución
Para hallar la constante del resorte
Con lo cual el modelo matemático es
Aplicando transformada
El 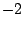 que acompaña a la función delta se debe a que el golpe es desde abajo con una intensidad de 2 unidades, además recuerde que que acompaña a la función delta se debe a que el golpe es desde abajo con una intensidad de 2 unidades, además recuerde que 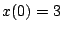 , pues el peso esta por debajo de la posición de equilibrio. Aplicando fracciones parciales , pues el peso esta por debajo de la posición de equilibrio. Aplicando fracciones parciales
De donde obtenemos que
Y así
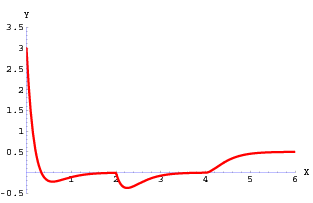
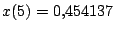 . La gráfica de . La gráfica de 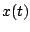 se muestra en la figura 1.12 se muestra en la figura 1.12
Revista digital Matemática, Educación e Internet.
|