|Instituto Tecnológico de Costa Rica|Escuela de Matemática|  M. Sc. Geovanni Figueroa M.

1 2  3  4  5  6  7  8  9  10  11  12  13  14  15  16

Circuitos L-R-C En un circuito L-R-C en serie la segunda ley de Kirchhoff establece que la suma de las caídas de tensión a través de un inductor, una resistencia y un capacitor es igual a la tensión aplicada $E(t)$. Sabemos que La caída de tensión a través de un inductor es $L \frac{di}{dt}$. La caída de tensión a través de la resistencia es $Ri$. La caída de tensión a través de un capacitor es $\frac{q}{c}$, pero como $$\frac{dq}{dt} = i(t) \Rightarrow q = \int_0^t i( \tau) d \tau$$ con lo cual la caída de tensión a través de un capacitor esta dada por $$\frac{1}{c} \int_0^t i( \tau) d \tau$$ donde $i(t)$ es la corriente y $L$, $R$ y $C$ son constantes conocidas como: la inductancia, la resistencia y la capacitancia, respectivamente. 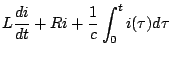Figura 1.13 De lo anterior obtenemos que la corriente $i(t)$ en un circuito como el de la figura 1.13 satisface la ecuación integrodiferencial $$L \frac{di}{dt} + Ri + \frac{1}{c} \int_0^t i( \tau) d \tau$$ la cual podemos resolver aplicando transformada de Laplace. Ejemplo Determine la corriente $i(t)$ en un circuito L-R-C en serie para el cual L=0.1H (Henrios), R=20 $\Omega$ (Ohms), C=$10^{-3}$ F (Faradios) y $i(0)=0$. La tensión $E(t)$ aplicada al circuito es la que se muestra en la figura 1.13. 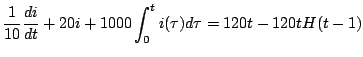Figura 1.14 Solución Puesto que la función se anula para $t \geq 1$, se puede escribir como $$E(t) = 120t - 120tH(t-1)$$ con lo cual la ecuación diferencial que modela este circuito es $$\frac{1}{10} \frac{di}{dt} + 20i + 1000 \int_0^t i( \tau) d \tau = 120t - 120t H(t-1)$$ Y al aplicar la transformada a ambos lados de la ecuación anterior, obtenemos que $$\frac{1}{10} sI(s) - i(0) + 20 I(s) + 1000 \frac{I(s)}{s} = 120 \left( \frac{1}{s^2} - \frac{e^{-s}}{s^2} - \frac{e^{-s}}{s} \right)$$ $$s^2 I(s) + 200s I(s) + 10000I(s) = 1200s \left( \frac{1}{s^2} - \frac{e^{-s}}{s^2} - \frac{e^{-s}}{s} \right)$$ $$\left(s + 100 \right)^2 I(s) = 1200 \left( \frac{1}{s} - \frac{e^{-s}}{s} - e^{-s} \right)$$ de donde obtenemos que $$I(s) = 1200 \left( \frac{1}{s(s+100)^2} - \frac{e^{-s}}{s(s+100)^2} + \frac{e^{-s}}{(s+100)^2} \right)$$ 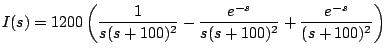Usando fraciones parciales tenemos que $$I(s) = \frac{3}{25} \left( \frac{1}{s} - \frac{1}{s+100} - \frac{100}{s(s+100)^2} \right.$$ $$- \left.\frac{e^{-s}}{s}+ \frac{e^{-s}}{s+100} + \frac{100e^{-s}}{(s+100)^2} - \frac{10000e^{-s}}{(s+100)^2} \right)$$ y al aplicar la transformada inversa $$i(t) = \frac{3}{25} \left( 1- H(t-1) - e^{-100t} + e^{-100t} H(t-1) \right)$$ $$- 12e^{-100t} - 1188(t-1)e^{-100(t-1)}H(t-1)$$ Subsecciones Sistemas de ecuaciones diferenciales       Inicio Revista digital Matemática, Educación e Internet.