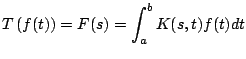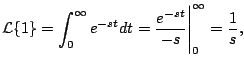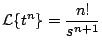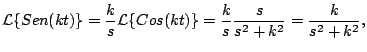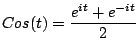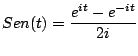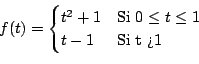|
Introducción
En el modelo matemático de un sistema físico, como el de una
masa  sujeta a un resorte o el de un circuito eléctrico en
serie, el lado derecho de la ecuación diferencial sujeta a un resorte o el de un circuito eléctrico en
serie, el lado derecho de la ecuación diferencial
es una función que representa una fuerza externa 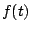 o un
voltaje o un
voltaje 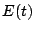 . Hasta ahora hemos resuelto problemas para los
cuales estas funciones eran continuas. Sin embargo, no es raro
encontrarse con funciones continuas a trozos; por ejemplo, en
circuitos eléctricos son muy comunes los voltajes dientes de
sierra o escalón. Es difícil, pero no imposible, resolver la
ecuación diferencial que describe el circuito en este caso, pero
la transformada de Laplace1.1 es una valiosa
herramienta para resolver problemas de este tipo. . Hasta ahora hemos resuelto problemas para los
cuales estas funciones eran continuas. Sin embargo, no es raro
encontrarse con funciones continuas a trozos; por ejemplo, en
circuitos eléctricos son muy comunes los voltajes dientes de
sierra o escalón. Es difícil, pero no imposible, resolver la
ecuación diferencial que describe el circuito en este caso, pero
la transformada de Laplace1.1 es una valiosa
herramienta para resolver problemas de este tipo.
Usaremos la transformada de Laplace en la solución de ecuaciones
integrales, de sistemas de ecuaciones diferenciales y también
la aplicaremos al cálculo de integrales.
En el capítulo anterior trabajamos con el operador derivación
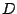 , el cual es un caso particular de funciones más generales
llamadas transformaciones lineales. Ahora estudiaremos una
nueva transformación lineal que es un caso especial de una clase
de transformaciones lineales de especial interés, llamadas
transformaciones integrales. Para comprender en qué consisten,
consideremos funciones , el cual es un caso particular de funciones más generales
llamadas transformaciones lineales. Ahora estudiaremos una
nueva transformación lineal que es un caso especial de una clase
de transformaciones lineales de especial interés, llamadas
transformaciones integrales. Para comprender en qué consisten,
consideremos funciones 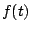 definidas en un intervalo finito o
infinito definidas en un intervalo finito o
infinito
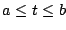 y tomemos una función fija y tomemos una función fija 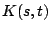 de variable
de variable 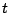 y parámetro y parámetro 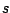 . Entonces, en general una
transformación integral tiene la forma . Entonces, en general una
transformación integral tiene la forma
La función 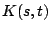 se llama núcleo de la transformación se llama núcleo de la transformación
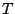 . Claramente . Claramente 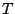 es lineal, sin importar la naturaleza de la
función es lineal, sin importar la naturaleza de la
función 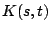 . El estudio de estas transformaciones
integrales generalizadas a conducido al análisis de ciertas
transformaciones específicas que han resultado de mucha utilidad
al abordar ciertos problemas. Una de estas transformaciones
especiales se obtiene haciendo . El estudio de estas transformaciones
integrales generalizadas a conducido al análisis de ciertas
transformaciones específicas que han resultado de mucha utilidad
al abordar ciertos problemas. Una de estas transformaciones
especiales se obtiene haciendo 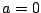 , ,
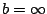 y y
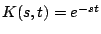 , como vemos en la siguiente definición. , como vemos en la siguiente definición.
|
|
Definición
[Transformada de Laplace]
|
| |
Suponga
que la función 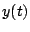 está definida para está definida para 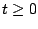 y la integral impropia y la integral impropia
converge para 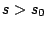 . Entonces la transformada de Laplace de . Entonces la transformada de Laplace de
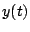 existe para existe para 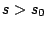 y está dada por y está dada por
|
Antes de dar alguna teoría que nos facilite el trabajo, vamos a
calcular la transformada de Laplace de algunas funciones, usando
esta definición.
Ejemplo
Calcule
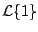 . .
Solución
Por definición
para 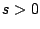 . .
Ejemplo
Calcule
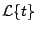 . .
Solución
Usando la definición
Observación: no resulta difícil intuir a partir de estos
ejemplos la siguiente transformada
para 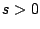 y y 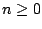 . Dejamos al lector la comprobación de
esta fórmula (sugerencia use inducción matemática). . Dejamos al lector la comprobación de
esta fórmula (sugerencia use inducción matemática).
Ejemplo
Calcule
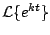 . .
Solución
Usando la definición
para 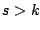 . .
Un par de transformadas particularmente útiles son las de las
funciones trigonométricas 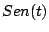 y y 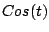 , que calculamos en
el siguiente ejemplo. , que calculamos en
el siguiente ejemplo.
Ejemplo
Calcule
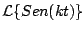 y y
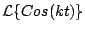 . .
Solución
Usando la definición
Por otro lado
De donde concluimos que
para 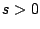 . .
Y retomando la transformada de 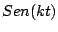
para 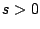 . .
Observación: podemos calcular la transformada 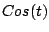 usando su representación compleja. Como
usando su representación compleja. Como
tenemos que
De forma análoga usando
podemos calcular
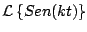 . .
Ejemplo
Calcule
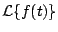 , donde , donde
Solución
Por definición
Revista digital Matemática, Educación e Internet.
|