|Instituto Tecnológico de Costa Rica|Escuela de Matemática|  M. Sc. Geovanni Figueroa M.

1 2  3  4  5  6  7  8  9  10  11  12  13  14  15  16

 

 

 

 

La transformada inversa de Laplace

Al aplicar la transformada de Laplace a una ecuación diferencial la convertimos en una ecuación algebraica, la cual podemos resolver para $Y(s)$, es decir, $Y(s) = G(S)$. Ahora, como ${\cal L} \{y(t) \} = Y(s)$ si pudiéramos devolvernos obtendríamos la solución $y(t)$ que buscamos. Es decir, necesitamos de la transformada inversa ${\cal L}^{-1} \{Y(s) \}$, para hallar la función $y(t)$

$$y(t) = {\cal L}^{-1} \{F(s) \} = {\cal L}^{-1} \{ G(s) \}$$

Entonces definamos la transformada inversa.

 

	Definición [Transformada inversa de Laplace]
	Si $F(s)$ es la transformada de Laplace de una función continua $f(t)$, es decir, ${\cal L} \{f(t) \} =F(s)$, entonces la transformada inversa de Laplace de $F(s)$, escrita ${\cal L}^{-1} \{ F(s) \}$ es $f(t)$, es decir, ${\cal L}^{-1} \{F(s) \} =f(t)$

 

Ejemplo
Calcule

$${\cal L}^{-1} \left\{ \frac{s}{s^2 + 4} \right\}$$

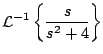
Solución
Puesto que

$${\cal L} \{ Cos(2t) \} = \frac{s}{s^2 + 4}$$

tenemos que

$${\cal L}^{-1} \left\{ \frac{s}{s^2 + 4} \right\} = Cos(2t)$$

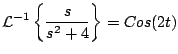
Observación existe un problema potencial al trabajar con la transformada inversa, puede no ser única. En efecto, es posible que ${\cal L} \{f(t) \} = {\cal L} \{ g(t) \}$, siendo $f(t) \neq g(t)$. Para nuestro propósito esto no es tan malo como parece, pues, si $f$ y $g$ son continuas y de orden exponencial en $[0,+ \infty[$ y ${\cal L} \{f(t) \} = {\cal L} \{ g(t) \}$, entonces $f(t)=g(t)$; pero, si $f$ y $g$ son continuas y de orden exponencial en $[0,+ \infty[$ y ${\cal L} \{ f(t) \} = {\cal } \{g(t) \}$, entonces se puede demostrar que las funciones $f$ y $g$ son casi iguales; esto quiere decir, que pueden diferir sólo en puntos de discontinuidad.

 

Ejemplo
Calcule ${\cal L} \{ f(t) \}$, donde $f(t)$ esta dada por

$$f(t) = \begin{cases} 1 & \text{Si $t \geq 0$, $t \neq 1$, $t\neq 2$\ } \\ 3 & \text{Si $t=1$} \\ 4 & \text{Si $t=2$} \\ \end{cases}$$

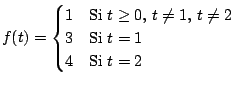
¿Qué se puede concluir ?

Solución

Usando la definición de transformada

$${\cal L} \{g(t) \} = \int_0^{\infty} e^{-st}g(t) dt$$

$$= \int_0^{\infty} e^{-st} dt$$

$$= -\frac{e^{-st}}{s} \biggr\vert^{\infty}_0$$

$$= \frac{1}{s}$$

Pero, anteriormente hemos comprobado que

$${\cal L} \{ 1 \} = \frac{1}{s}$$

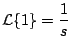
con lo cual las funciones $f(t)$ y $g(t)$ tienen la misma transformada, de este modo, la transformada inversa de

$$F(s)=\frac{1}{s}$$

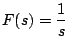
no es única.

El siguiente resultado establece el comportamiento de $F(s)$ en infinito.

	Teorema [Comportamiento de $F(s)$ en infinito]
	Sea $f: [0,+\infty[ \rightarrow$   $\mbox{$I \hspace{-1.3mm} R$}$$$ una función continua a trozos y de orden exponencial en $[0,+ \infty[$, entonces $$\lim_{s \rightarrow \infty} {\cal L} \{ f(t) \} = \lim_{s \rightarrow \infty} F(s) = 0$$

Demostración

Puesto que $f(t)$ es continua a trozos en $[0,+ \infty[$ necesariamente es acotada en este intervalo; o sea, $\Vert f(t) \Vert < M$ para todo $t \in [0,\infty[$. De donde

$$\biggr\vert {\cal L} \left\{ f(t) \right\} \biggr\vert \leq \int_... ... \mid e^{-st} dt = -M \frac{e^{-st}}{s} \biggr\vert _0^{\infty} = \frac{M}{s}$$

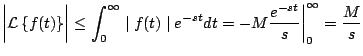
y así $\mid {\cal L} \left\{ f(t) \right\} \mid \rightarrow 0$ cuando $s \rightarrow \infty$, de modo que ${\cal L} \left\{ f(t) \right\} \rightarrow 0$ cuando $s \rightarrow \infty$.

 

Observación: el resultado anterior es válido independientemente de que $f(t)$ sea continua a trozos o de orden exponencial, basta con que $F(s)$ existe.

Ejemplo
¿ Porqué no existe una función $f(t)$ tal que ${\cal L} \{ f(t) \} = \frac{s}{s+1}$ ?

Solución
Suponga que existe, entonces por el teorema anterior

$$\lim_{s \rightarrow \infty} \frac{s}{s+1} = 0$$

lo cual es falso; por lo tanto no existe tal función.

Observación: con un argumento similar podemos concluir que no existen una función $f(t)$ tal que $F(s)=1$, $F(s) = s^2$, $F(s)=Sen(s)$, $F(s)=Ln(s)$, es decir, estas funciones no tienen transformada inversa. Por otro lado, una función racional $F(s)=\frac{P(s)}{Q(s)}$ es la transformada de alguna función $f(t)$ si el grado del numerador $P(s)$ es menor que la del denominador $Q(s)$.

Los siguientes resultados son útiles en análisis de sistemas de control automático, especialmente cuando se trazan gráficas.

 

	Teorema [Del valor inicial]
	Si ${\cal L} \left\{ f(t) \right\}=F(s)$ y $\lim_{t \rightarrow 0^+} f(t)$ existe y es igual a $f(0)$,  entonces $$\lim_{t \rightarrow 0} f(t) = \lim_{s \rightarrow + \infty} sF(s)=f(0)$$

 

Demostración:
Como

$${\cal L} \left\{f^{\prime}(t) \right\} = sF(s) - f(0)$$

y

$$\lim_{s \rightarrow + \infty} {\cal L} \left\{ f^{\prime}(t) \right\} = 0$$

siempre y cuando $f^{\prime}(t)$ sea continua a trozos y de orden exponencial. Tenemos que

$$\lim_{s \rightarrow + \infty} sF(s) = f(0) = \lim_{t \rightarrow 0^+} f(t)$$

siempre y cuando $f(t)$ sea continua por la derecha en $t=0$.

 

Ejemplo
Si $f(t)=Cos(t)$, calcule $\lim_{s \rightarrow \infty} sF(s)$.

Solución
Usando el teorema del valor inicial

$$\lim_{s \rightarrow \infty} sF(s) = f(0) = 1$$

Note que no fue necesario calcular $F(s)$.

 

	Teorema [Del valor final]
	Si ${\cal L} \left\{ f(t) \right\}=F(s)$ y el límite $\lim_{t \rightarrow \infty} f(t)$ existe, entonces $$\lim_{t \rightarrow + \infty} f(t) = \lim_{s \rightarrow 0} sF(s)$$

Demostración:
Análoga a la anterior.

El siguiente teorema establece la linealidad de la transformada inversa.

 

	Teorema [Linealidad de la transformada inversa]
	Sean $f$ y $g$ funciones continuas a trozos y de orden exponencial en el intervalo $[0,+ \infty[$ tales que ${\cal L} \{f(t) \} =F(s)$ y ${\cal L} \{ g(t) \} = G(s)$ , entonces $${\cal L}^{-1} \{ \alpha F(s) + G(s) \} = \alpha {\cal L}^{-1} \{F(s) \} + {\cal L}^{-1} \{G(s) \}$$ $$= \alpha f(t) + g(t)$$

Ejemplo
Calcule

$${\cal L}^{-1} \left\{ \frac{4s}{\left(s - 2 \right) \left( s^2 + 4 \right)} \right\}$$

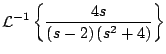
Solución

Para usar la propiedad de linealidad de la transformada inversa de Laplace primero debemos expandir

$$\frac{4s}{\left(s - 2 \right) \left( s^2 + 4 \right)}$$

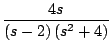
en fraciones parciales

$$\frac{1}{s-2} - \frac{s}{s^2 + 4} + \frac{2}{s^2 + 4}$$

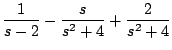
ahora sí

$${\cal L}^{-1} \left\{ \frac{4s}{\left(s - 2 \right) \left( s^2 + 4 \right)} \right\} = {\cal L}^{-1} \left\{ \frac{1}{s-2} \right\} - {\cal L}^{-1} \left\{ \frac{s}{s^2 + 4} \right\} + {\cal L}^{-1} \left\{ \frac{2}{s^2 + 4} \right\}$$

$$= e^{2t} - Cos(2t) + Sen(2t)$$

El siguiente ejemplo ilustra el proceso que vamos a usar en la solución de ecuaciones diferenciales mediante Laplace. Es un ejemplo que puede ser resuelto de manera más eficiente con las técnicas ya estudiadas, pero el objetivo es aplicar algunas de las propiedades enunciadas hasta ahora e introducir la técnica de solución de ecuaciones diferenciales.

Ejemplo
Use la transformada de Laplace para resolver el problema de valor inicial

$$\left\{ \begin{array}{rcl} y^{\prime} - 3y & = & e^{2t} \\ y(0) & = & 1 \\ \end{array} \right.$$

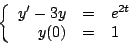
Solución

Aplicando transformada de Laplace a ambos lados de la ecuación diferencial

$${\cal L} \{y^{\prime} - 3y \} = {\cal L} \{ e^{2t} \}$$

$${\cal L} \{ y^{\prime} \} - 3 {\cal L} \{ y \} = \frac{1}{s-2}$$

$$sY(s)- y(0) - 3Y(s) = \frac{1}{s-2}$$

$$sY(s)- 1 - 3Y(s) = \frac{1}{s-2}$$

$$Y(s) = \frac{s-1}{(s-2)(s-3)}$$

$$Y(s) = -\frac{1}{s-2} + \frac{2}{s-3}$$

Ahora debemos de aplicar transformada inversa para hallar $y(t)$

$${\cal L}^{-1} \{Y(s) \} = -{\cal L}^{-1} \left\{ \frac{1}{s-2} \right\} + 2 {\cal L}^{-1} \left\{ \frac{1}{s-3} \right\}$$

$$y(t) = -e^{2t} + e^{3t}$$

Observación: está ecuación diferencial puede resolverse como una ecuación lineal con factor integrante $\mu(t)=e^{-3t}$.

 

Inicio Revista digital Matemática, Educación e Internet.