|Instituto Tecnológico de Costa Rica|Escuela de Matemática| M. Sc. Geovanni Figueroa M.

1 2  3  4  5  6  7  8  9  10  11  12  13  14  15  16

 

 

 

 

Función impulso unitario

Algunos sistemas mecánicos suelen estar sometidos a una fuerza externa (o a una tensión eléctrica en el caso de los circutitos eléctricos) de gran magnitud, que solamente actúa durante un tiempo muy corto. Por ejemplo, una descarga elétrica podría caer sobre el ala vibrante de un avión; a un cuerpo sujeto a un resorte podría dársele un fuerte golpe con un martillo, una pelota (de beisbol, de golf o de tenis) inicialmente en reposo, podría ser enviada velozmente por los aires al ser golpeada con violencia con un objeto como una bat de beisbol, un bastón de golf o una raqueta de tenis. La función impulso unitario puede servir como un modelo para tal fuerza.

 

	Definición [Impulso unitario]
	La función $\delta_a : [0,+\infty[ \rightarrow$   $\mbox{$I \hspace{-1.3mm} R$}$$$ dada por $$\delta_a(t - t_0) = \begin{cases} 0 & \text{Si $0 \leq t ... ... \leq t_0+a$} \\ 0 & \text{Si $t \geq t$} \\ \end{cases}$$

donde $a > 0$, $t_0>0$ se conoce como la función impulso unitario. La gráfica de la función escalón para $a=0.5$ y $t_0=2$ se muestra en la figura 1.8.

Observación: para valores pequeños de $a$, se tiene que $\delta_a(t-t_0)$ es una función constante de gran magnitud que esta activa por un tiempo muy corto alrededor de $t_0$.

Figura 1.8

 

	Teorema [Area bajo la función impulso]
	La función impulso unitario satisface la propiedad $$\int_0^{\infty} \delta_a(t-t_0) dt = 1$$

y de aquí su nombre.

Demostración

$$\int_0^{\infty} \delta_a(t-t_0) dt = \int_0^{t_0-a} 0 \cdot dt + \int_{t_0-a}^{t_0+a} \frac{1}{2a} \cdot dt + \int_{t_0+a}^{\infty} 0 \cdot dt$$

$$= 0 + \frac{2a}{2a} + 0$$

$$= 1$$

 

En la práctica es conveniente trabajar con otro tipo de impulso llamado función de Dirac^1.3

 

	Definición [Función delta de Dirac]
	La función delta de Dirac esta dada por $$\lim_{a \rightarrow 0} \delta_a(t-t_0) = \delta(t-t_0)$$

Observación: la función delta de Dirac, no es una función, realmente es lo que se conoce como una función generalizada (o distribución).

 

	Teorema [Propiedades de la función delta]
	La función delta de Dirac satisface las siguientes propiedades $$\delta(t-t_0) = \begin{cases} \infty & \text{Si $t = t_0$... ...nd{cases} \hspace{1cm} \int_0^{\infty} \delta(t-t_0) dt = 1$$

El siguiente teorema establece la transformada de Laplace de la función delta de Dirac.

 

	Definición [Transformada de delta]
	Para $t_0>0$ $${\cal L} \{\delta(t-t_0) \} = e^{-st_0}$$

Demostración
Para iniciar la prueba debemos escribir la función impulso unitario en términos de la función escalón unitario

$$\delta_a(t-t_0) = \frac{1}{2a} \left( H(t - (t_0-a)) - H(t-(t_0 + a)) \right)$$

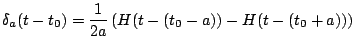
De donde tenemos que

$${\cal L} \left\{ \delta_a \left(t - t_0 \right) \right\} = \frac{1}{2a} {\cal L} \left\{ H(t - (t_0-a)) \right\} - \frac{1}{2a} \left\{ H(t-(t_0 + a)) \right\}$$

$$= \frac{1}{2a} \left( \frac{e^{-s(t_0-a)}}{s} \right) - \frac{1}{2a} \left( \frac{e^{-s(t_0+a)}}{s} \right)$$

$$= e^{-st_0} \left( \frac{e^{sa} - e^{-sa}}{2sa} \right)$$

con lo cual

$${\cal L} \left\{ \delta(t - t_0) \right\} = {\cal L} \left\{ \lim_{a \rightarrow 0} \delta_a(t- t_0) \right\}$$

$$= \lim_{a \rightarrow 0} {\cal L} \left\{ \delta_a(t- t_0) \right\}$$

$$= \lim_{a \rightarrow 0} e^{-st_0} \underbrace{\left( \frac{e^{sa} - e^{-sa}}{2sa} \right)}_{L'H \hat{o}pital}$$

$$= e^{-st_0} \lim_{a \rightarrow 0} \frac{se^{sa} + se^{-sa}}{2s}$$

$$= e^{-st_0}$$

 

Observación: a partir de ${\cal L} \left\{ \delta(t-t_0) \right\} =e^{-st_0}$ es razonable concluir que ${\cal L} \left\{ \delta(t) \right\}=1$. Esto reafirma el hecho de que $\delta(t)$ no es una función ordinaria, puesto que se espera que ${\cal L} \{ f(t) \}$ cuando $s \rightarrow \infty$.

Ejemplo
Calcule ${\cal L} \{ \delta(t-2 \pi) \}$

Solución
Claramente

$${\cal L} \{ \delta(t - 2 \pi) \} = e^{-2 \pi s}$$

 

 

 

Revista digital Matemática, Educación e Internet.