¿Sabe lo que es la altura de un triángulo?  Si ya lo sabe, perfecto; y si no, no se preocupe.

En el siguiente apartado se tratará de construir la definición de altura, y algo más, ortocentro.

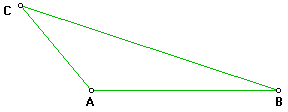
Actividad

Contrucción de las alturas y el ortocentro de cualquier triángulo con papel, lápiz, regla, compás y transportador.

1  Dibuje cualquier triángulo; nombre sus vértices como A, B y C, respectivamente.

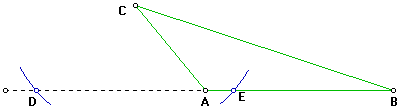
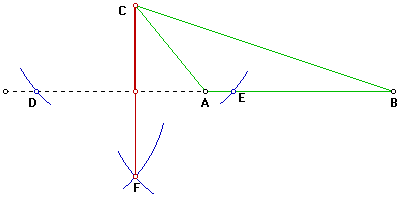
2  Seleccione el vértice C.  Utilizando el compás y con centro en el vértice seleccionado, trace un par de arcos que intersequen al lado opuesto (o una prolongación de este), nombre estos puntos como  D y E.

3  Con centro en D y utilizado la misma abertura del compás del paso anterior, trace un arco por debajo del segmento AB (o prolongación de este).

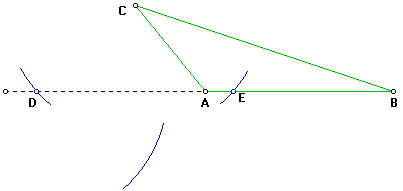
4  Con centro en E y utilizado la misma abertura del compás del paso anterior, trace un arco que interseque al arco del paso anterior. 

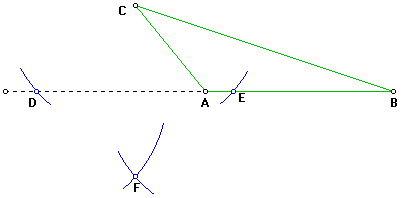
5  Trace el segmento  que une el vértice C con el vértice F.  Repinte un poco fuerte el segmento que va desde C hasta el segmento AB (o prolongación de este).  Este último segmento, corresponde a la altura del DABC sobre el lado AB (o prolongación de este).

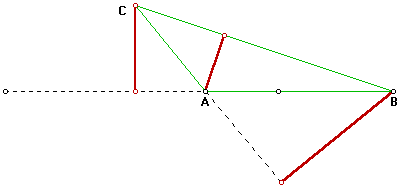
6  Repita el procedimiento anterior utilizado el vértice A y luego el vértice B.

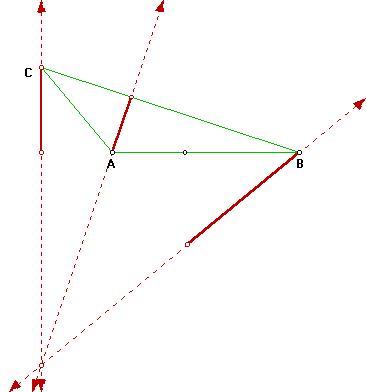
7  ¿Cuál cree que sea la definición de altura?

Sugerencia:  Utilizando un tranportador, mida los águlos formados por la altura y el segmento al que interseca (o prolongación de este).

8  Prolongue las alturas hasta que estas se intersequen.  ¿Descubrió alguna relación entre la intersección de las tres alturas?  Si no fue así, es muy probable que haya movido la abertura del compás o que los instrumentos que utiliza no sean muy precisos.

Observe si lo que descubrió concuerda con lo siguiente:

Teorema

En todo triángulo se cumple que las tres alturas son concurrentes, o sea, se intersecan en un mismo punto.

 

Definición

El punto de intersección de las tres alturas recibe el nombre de ortocentro.

Aún  falta construir la definición de altura; para ello realice lo siguiente.

Actividad Interactiva

Contrucción de las alturas. 

1  Construya las alturas del DABC, dando clic sobre cada uno de los botones de la parte izquierda.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

2  ¿Cuánto miden los ángulos formados por las alturas, y los segmentos a los que interseca cada una de ellas?  Mueva los vértices rojos para ver si cumple su hipótesis.

3  Defina, con sus propias palabras, altura de un triángulo.

4  ¿El ortocentro de un triángulo cualquiera siempre está dentro del mismo?  Mueva los vértices e investigue lo que sucede.  ¿Qué concluye?

5  ¿Dónde se ubica el ortocentro si el triángulo es rectángulo?  Mueva los vértices y basándose en la información de la medida de los ángulos, haga coincidir dos de las alturas con dos de los lados del triángulo.  ¿Qué concluye?

6  Utilice los botones Reiniciar y Animación cuando lo crea conveniente.

Compare sus conclusiones con las siguientes.

Definición

La altura es el segmento que va de un vértice y cae perpedicularmente sobre el lado opuesto (o prolongación de este).

 

El ortocentro de un triángulo no siempre se halla en el interior de este.  Si el triángulo es rectángulo, el ortocentro se ubicará sobre la intersección de los catetos.