Además de sus propiedades con respecto a la medida de sus lados, los triángulos equiláteros e isósceles poseen varias propiedades con respecto a las medidas de sus ángulos

Triángulo Isósceles

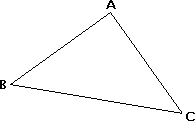
Este triángulo tiene, como ya se sabe, dos lados de igual medida, como ejemplo puede observarse la figura siguiente :

En este triángulo, el lado AB tiene la misma medida del AC, por lo que el ΔABC se clasifica como isósceles.

Ahora bien, se  sabe que a lados iguales de un triángulo se oponen ángulos congruentes y por tener el ΔABC dos lados iguales entonces a estos se opondrán dos ángulos congruentes.

Esto significa que en todo triángulo isósceles hay dos ángulos congruentes que se oponen a los lados de igual medida.  Debido a esto, se puede asegurar que en el triángulo que aparece al inicio de esta página, los ángulos ABC y ACB tienen la misma medida.

Actividad Interactiva

1. Mueva los puntos en rojo y observe las medidas que se aprecian  en la figura de la derecha.

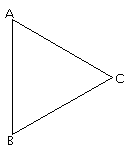
2. ¿Qué clase de triágulo es el de la derecha según sus lados?

3. ¿Se comprueba lo señalado anteriormente, de acuerdo con las medidas de los ángulos opuestos a los lados de igual medida del triángulo ΔABC?

Nota: Para volver a la figura inicial presione la tecla R.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

Laboratorio

Trabaje con papel.

1. En una hoja de papel construya un triángulo isósceles, ( ΔABC, con los lados AB y AC de igual medida).

2. Ahora trace la altura sobre el lado BC.

3. Trace la mediatriz de este lado.

4. Trace la bisectriz del ángulo BAC.

5. Por último, debe trazar la mediana sobre el lado BC .

6. ¿Qué conclusión puede obtener de lo anterior?

Para finalizar, después de haber realizado el laboratorio anterior la conclusión más evidente a la que puede llegar es que las rectas notables trazadas sobre el lado desigual coinciden.

Triángulo Equilátero

En este tipo de triángulos los lados miden lo mismo y además los tres ángulos interiores tienen la misma medida (60º).  Como ejemplo se muestra la siguiente figura:

Laboratorio

Trabaje con papel.

1. Dibuje un triángulo equilátero en una hoja de papel.

2. Trace las bisectrices del triángulo.

3. Trace las mediatrices del triángulo equilátero.

4. Trace las medianas del triángulo.

5. Trace las alturas del triángulo.

6. ¿Qué conclusión obtiene?

7. Observe los puntos de intersección de cada uno de los grupos de rectas notables.

8. ¿Qué observa?  ¿Qué puede concluir?

En todo triángulo equilátero las rectas notables coinciden y los puntos de intersección de ellas también coinciden en un único punto.