¿Sabía usted que todo cuerpo se equilibra en su centro de gravedad?

Pues sí, el famoso matemático Isaac Newton, comprobó que todo cuerpo puede ser mantenido en equilibrio y sin girar si se coloca apropiadamente.

A continuación, se trabajará para encontrar el centro de gravedad de los triángulos.

Laboratorio

Trabaje con papel.

Dibuje y recorte un triángulo como el que se muestra en la figura de la izquierda.

Debe doblar sobre un lado, uniendo vértice con vértice como se muestra en la figura de la derecha.

 

 

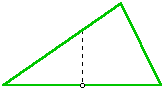
Con los pasos anteriormente realizados, ha encontrado el punto medio de un lado del triángulo.

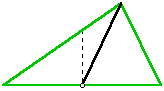
Ahora debe trazar el segmento desde ese punto medio hasta el vértice opuesto a éste, como se muestra en la figura de la derecha.

Definición

El segmento que une el punto medio de un lado de un triángulo y el vértice opuesto a éste recibe el nombre de mediana.

 

¿Cuántas medianas se podrán trazar en un triángulo?

La respuesta es tres, esto debido a que todo triángulo tiene tres vértices, por lo que sólo se pueden trazar igual número de medianas, una por cada uno de los vértices.

 

Laboratorio

Trabaje con papel.

1. Dibuje un triángulo en una hoja de papel y recórtelo.

2. Uniendo los vértices respectivos halle los puntos medios de cada uno de los lados del triángulo.

3. Ahora debe trazar (con un lapicero) las tres medianas del triángulo.

4. ¿Existirá alguna relación entre las tres medianas?

Teorema

En todo triángulo se cumple que las tres medianas son concurrentes, o sea, se intersecan en un mismo punto.

 

Definición

El punto de intersección de las tres medianas de un triángulo recibe el nombre de baricentro.

Actividad Interactiva

Construcción de las medianas de un triángulo con regla y compás.

Nota: Para volver a la figura inicial presione la tecla R.

Realize la siguiente actividad, con ayuda del cuadro de trabajo que se presenta abajo, dando clic en los botones que van apareciendo.

1.  Construya el ΔABC.

 

2.  Debe trazar un círculo (con el compás) que tenga centro en B y con un radio (indicado por la abertura del compás) mayor que la mitad del lado BC.

3.  Ahora trace un círculo con centro en C, que tenga el mismo radio que el círculo anteriormente construido (esto se logra sin modificar la abertura del compás).

4.  Trace el segmento que une los dos puntos de intersección de los círculos y marque la intersección de este segmento con el lado BC (note que este punto es el punto medio del segmento BC).

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

 

5.  Trace la mediana, es el segmento que une ese punto medio del lado con el vértice opuesto a este (el punto A).

6.  Debe realizar los pasos 2, 3, 4 y 5 para encontrar las otras dos medianas del triángulo y, por último, marcar el punto de intersección de estas (baricentro).

 

Mueva los puntos que están en rojo y observe que para todo triángulo que se forma, se cumple que las medianas son concurrentes y que además el baricentro siempre queda dentro del triángulo.