|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
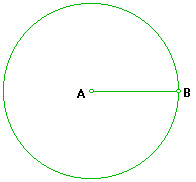
En el siguiente apartado, se estudiará una característica muy especial que poseen los triángulos equiláteros. Laboratorio Trabaje con papel; construcción de un triángulo equilátero con papel, lápiz, regla y compás. 1. Dibuje un segmento (no muy pequeño) y proceda a nombrar sus extremos como A y B.
2. Use el compás; con centro en A, trace un círculo de radio AB .
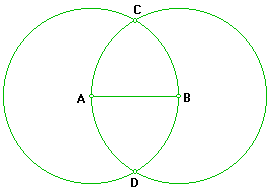
3. Use el compás; con centro en B, trace un círculo de radio BA . Marque los puntos de intersección de los círculos y nómbrelos como C y D respectivamente.
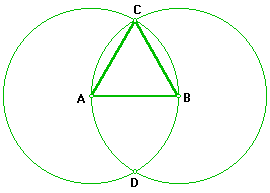
4. Trace los segmentos AC y BC . El DABC es equilátero; si se utiliza el punto D también se obtiene un triángulo equilátero.
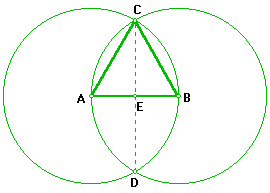
5. Trace una línea punteada desde C hasta D y marque el punto de intersección con el segmento AB, nombre con E este punto.
6. Trace la altura, la bisectriz, la mediana y la mediatriz del DABC, utilizando para ello el vértice C. La altura ya la construyó, repinte el segmento CE . 7. ¿Qué concluye luego de haber realizado la actividad 6? Repita la actividad 6 utilizando el vértice A y luego el vértice B. 8. ¿Se confirmó su conclusión de del paso anterior?
Actividad Interactiva 1. Escoja uno de los vértices, dando clic sobre alguno de los botones de la parte superior del campo de trabajo. 2. Dé clic sobre: Trazar altura, Trazar Mediana, Trazar Mediatriz, y por último, sobre, Trazar Bisectriz. Se sugiere ese orden.
Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado
3. Mueva los vértices rojos del DABC. 3.1 ¿Qué característica poseen la altura, la mediana, la mediatriz y la bisectriz? 3.2 Si desea ver una animación de los vértices, dé un clic sobre el botón de Animación. Para detener la animación, vuelva a dar clic sobre el mismo botón. 3.3 Si desea repetir la actividad con el mismo vértice, dé un clic sobre Reiniciar. 3.4 ¿Cuál es su conclusión, acerca de la pregunta planteada en 3.1?
Compare su conclusión con la siguiente. En general se dice que, en un triángulo equilátero la altura, mediana, mediatriz y bisectriz desde un mismo vértice coinciden. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||