Perímetro de un triángulo

El perímetro de un ∆ABC se obtiene al sumar las longitudes de sus tres lados y generalmente se denota con la letra P.

P = |AB| + |AC| + |BC|

Ejemplo

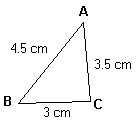
En la figura de la derecha se tiene que el perímetro está dado por la suma de sus lados, o sea,

P = 4.5 + 3 + 3.5 = 11cm

Altura de un triángulo

Es el segmento que parte desde un vértice del triángulo y que es perpendicular al lado opuesto o a su prolongación.

Área de un triángulo

Calcular el área de ciertas figuras resulta muy fácil, como en el caso del siguiente cuadrado.

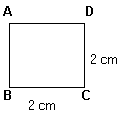
ya que se puede dividir el cuadrado en unidades cuadradas.

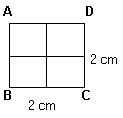
Se puede observar que este cuadrado tiene un área de 4cm².

Ahora, considere los triángulos formados al trazar una diagonal del cuadrado.

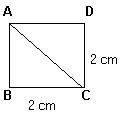
Y tome uno de ellos.

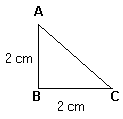
Es claro que el área de este triángulo es la mitad del área del cuadrado, o sea 2cm².

Note que AB   |   BC, por lo que en el triángulo ABC el segmento BC puede tomarse como la base y el segmento AB como la altura asociada.

Al realizar la siguiente operación  se obtiene como resultado 2cm², o sea, el área del triángulo.

¿Sucederá esto en todos los casos?

La respuesta es sí, ya que en todo triángulo se cumple que , donde b=base y h=altura.

Con la fórmula anterior para obtener el área, únicamente se necesita la longitud de un lado y la altura correspondiente a ese lado.

Fórmula de Herón

¿Qué pasa si lo que se conoce es la longitud de los tres lados?

¿Se podrá calcular el área del triángulo ?

¿Será posible hallar el área de un triángulo conociendo únicamente las medidas de sus lados?

Se sabe que el área de este triángulo de la izquierda está dada por cm².

Ahora realice el siguiente proceso

• Obtenga el semiperímetro del triángulo, dividiendo el perímetro entre 2, denótelo con S.

• Reste al semiperímetro cada una de las medidas de los lados del triángulo.

(6-5) = 1

(6-4) = 2

(6-3) = 3

• Multiplique el semiperímetro por cada uno de los resultados anteriores.

S(S-3)(S-5)(S-4) = 6(6-3)(6-5)(6-4) = 6(3)(1)(2) = 36

• Tome la raíz cuadrada de ese resultado.

¿Será una simple casualidad que el área del triángulo sea igual a ?

Experimente con otros triángulos en el siguiente cuadro.

Nota: Para volver a la figura inicial presione la tecla R.

Usted puede mover los vértices del triángulo para observar el  resultado con otros triángulos.

Los navegadores ya no brindan soporte para applets de java, este applet se ha deshabilitado

 Efectivamente, siempre se cumple que en todo ∆ABC el área es igual a: