|
|
Teoremas sobre límites infinitos
|
|
Teorema
12
|
|
|
Si  es cualquier entero positivo, entonces se cumple que: es cualquier entero positivo, entonces se cumple que:
-

-
 si si  es par es par
-
 si si  es impar es impar
Prueba:
Al final del capítulo.
|
|
Ejemplos:
-
 en
este caso en
este caso 
-
 con con 
Gráficamente se tiene que:
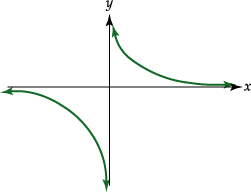
-

-

-

-

Ejercicio:
Determine cada uno de los límites siguientes:
-

-

-

Ejemplos: de cada uno de los casos que se mencionan en el
teorema anterior.
-

Observe que si se hiciera la sustitución directa se obtiene la
forma indeterminada
 . .
Como la expresión  puede aproximarse a cero a través de
valores positivos o a través de valores negativos, estudiaremos
los límites laterales como sigue: puede aproximarse a cero a través de
valores positivos o a través de valores negativos, estudiaremos
los límites laterales como sigue:
-
| a. |
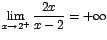 |
Como
 , entonces , entonces
 por lo que por lo que
 y se dice que
y se dice que
 . Así, el numerador tiende a
una constante positiva y el denominador tiende a . Así, el numerador tiende a
una constante positiva y el denominador tiende a
 . .
Luego, aplicando la parte 1 del teorema se obtiene que

|
b. |
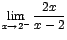 |
-
Como
 , entonces , entonces
 por lo que por lo que
 y se tiene que
y se tiene que
 . Como el numerador tiende a
una constante positiva y el denominador tiende a . Como el numerador tiende a
una constante positiva y el denominador tiende a
 aplicando la parte 2 del teorema anterior se obtiene que aplicando la parte 2 del teorema anterior se obtiene que

Como los límites laterales son diferentes decimos que
 no existe. no existe.
-
-

Observe que
 y que y que

Como la expresión
 puede tender hacia cero a través de valores positivos o a través
de valores negativos debemos calcular los límites laterales de la siguiente
forma: puede tender hacia cero a través de valores positivos o a través
de valores negativos debemos calcular los límites laterales de la siguiente
forma:
| a. |
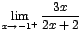 |
-
Como
 entonces entonces
 por lo que por lo que
 y y
 de donde de donde
 . .
Así el numerador tiende a una constante negativa y el
denominador tiende a
 , por lo que aplicando la parte 3
del teorema anterior se obtiene que , por lo que aplicando la parte 3
del teorema anterior se obtiene que

- b.
|
 |
-
Como
 entonces entonces
 y y
 de donde de donde
 y puede decirse que y puede decirse que
 . .
Luego, el numerador tiende a una constante negativa y el
denominador tiende a
 , por lo que aplicando la parte 4
del teorema anterior se obtiene que , por lo que aplicando la parte 4
del teorema anterior se obtiene que

Como
 entonces entonces
 no existe. no existe.
Ejercicio:
Calcular cada uno de los límites siguientes:
-

-

Ejemplos:
| a. |
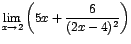 |
-
En este caso
 y y
 pues pues
 y en el numerador se tiene una
constante positiva, obteniéndose el resultado anterior al
aplicar la parte
1 del teorema 13. y en el numerador se tiene una
constante positiva, obteniéndose el resultado anterior al
aplicar la parte
1 del teorema 13.
Luego:

-
| b. |
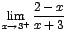 |
-
-
Este límite anterior puede escribirse como
 siendo siendo  y y

Calculamos el

Como
 entonces entonces
 y y
 ; además la constante en el
numerador es positiva por lo que aplicando la parte 1 del teorema
13 se tiene que ; además la constante en el
numerador es positiva por lo que aplicando la parte 1 del teorema
13 se tiene que

Ahora, el
 y
aplicando la parte 2 del teorema anterior se tiene que y
aplicando la parte 2 del teorema anterior se tiene que
![$\displaystyle {\lim_{x \rightarrow{3^{+}}}{\left[(2-x)\cdot
\frac{1}{x+3}\right]}=+\infty}$](img656.gif)
-
- c.
|
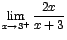 |
-
Este límite puede escribirse como
![$\displaystyle {\lim_{x \rightarrow{3^{+}}}{\left[2x\cdot \frac{1}{x+3}\right]}}$](img658.gif) sabemos que
sabemos que
 y
además y
además
 por lo que
aplicando la parte 3 del teorema anterior concluimos que por lo que
aplicando la parte 3 del teorema anterior concluimos que

| d. |
![$\displaystyle {\lim_{x \rightarrow{1^{+}}}{\left[\frac{2x+3}{\frac{1}{x-1}}\right]}}$](img662.gif) |
-
-
En este caso se tiene que
 y que y que
 por parte 1 del
teorema 13 de donde, aplicando la parte d) del teorema 14 concluimos que por parte 1 del
teorema 13 de donde, aplicando la parte d) del teorema 14 concluimos que
![$\displaystyle {\lim_{x \rightarrow{1^{+}}}{\left[\frac{2x+3}{\frac{1}{x-1}}\right]}=0}$](img665.gif)
Ejemplos:
-
![$\displaystyle {\lim_{x \rightarrow{2}}{\left[\frac{1}{\frac{x}{2}-1}+4x\right]}}$](img668.gif)
En este caso  y y

Calculemos

Si
 entonces entonces
 por lo
que puede decirse que por lo
que puede decirse que

Como la constante en el numerador es positiva, aplicando la parte
2 del teorema 13 se deduce que:

Por otra parte
 , y aplicando el punto
1 del teorema 15 se obtiene que , y aplicando el punto
1 del teorema 15 se obtiene que
![$\displaystyle {\lim_{x \rightarrow{2^-}}{\left[\frac{1}{\frac{x}{2}-1}+4x\right]}=-\infty}$](img676.gif)
-

Este límite puede escribirse como
![$\displaystyle {\lim_{x \rightarrow{2^{-}}}{\left[3x\cdot\frac{1}{\frac{x}{2}-1}\right]}}$](img678.gif)
Como
 y y
 , aplicando la parte 2 del teorema 15 se obtiene que
, aplicando la parte 2 del teorema 15 se obtiene que

-

El límite anterior puede escribirse como
![$\displaystyle {\lim_{x \rightarrow{2^{-}}}{\left[(1-4x)\cdot\frac{1}{\frac{x}{2}-1}\right]}}$](img683.gif)
Como
 , y , y
 ,
entonces aplicando el punto 3 del teorema 15 se obtiene que ,
entonces aplicando el punto 3 del teorema 15 se obtiene que

-

En este caso se tiene que
 y y
 por parte 2
del teorema 13 (compruébelo). Luego aplicando el punto 4 del
teorema 15 se tiene que por parte 2
del teorema 13 (compruébelo). Luego aplicando el punto 4 del
teorema 15 se tiene que

Ejercicios:
aplicación de los teoremas 13,14 y 15
Calcule los límites siguientes:
-

-

-

Ejemplo:
Determinar el límite siguiente
![$\displaystyle {\lim_{x \rightarrow{2^{+}}}{\left[\frac{2}{(x-2)^{2}}+\frac{x+1}{\sqrt{x-2}}\right]}}$](img697.gif)
En este caso calculemos:
 y y

Como
 entonces entonces  y y  por lo
que por lo
que  y y  o sea o sea
 y y
 . Luego, se tiene que . Luego, se tiene que
 y y
 (por
teorema 13), y concluimos de acuerdo al teorema anterior que: (por
teorema 13), y concluimos de acuerdo al teorema anterior que:
![$\displaystyle {\lim_{x \rightarrow{2^{+}}}{\left[\frac{2}{(x-2)^{2}}+\frac{x+1}{\sqrt{x-2}}\right]}=+\infty}$](img706.gif)
![$\displaystyle {\lim_{x \rightarrow{2^{+}}}{\left[\frac{2}{(x-2)^{2}}\cdot \frac{x+1}{\sqrt{x-2}}\right]}=+\infty}$](img707.gif)
Ejercicio
Calcule cada uno de los límites siguientes:
-
![$\displaystyle {\lim_{x \rightarrow{1^{-}}}{\left[\frac{3x}{2-2x}+\frac{5}{x-1}\right]}}$](img708.gif)
-
![$\displaystyle {\lim_{x \rightarrow{1^{-}}}{\left[\frac{15x}{(2-2x)(x-1)}\right]}}$](img709.gif)
Ejemplo:
Calculemos:
 y y

Como
 entonces entonces  por lo que por lo que
 , o sea , o sea
 y y
 . Luego, se tiene que . Luego, se tiene que
 (por teorema
13 parte 2) y (por teorema
13 parte 2) y
 (por
teorema 13 ). (por
teorema 13 ).
Entonces, utilizando el teorema anterior se tiene que:
![$\displaystyle {\lim_{x \rightarrow{-3^{-}}}{\left[\frac{2-x}{(x+3)}+\frac{2x}{(x+3)^{2}}\right]}=-\infty}$](img722.gif) y y
![$\displaystyle {\lim_{x \rightarrow{-3^{-}}}{\left[\frac{2-x}{x+3}\cdot \frac{2x}{(x+3)^{2}}\right]}=+\infty}$](img723.gif)
Ejercicio
Calcule los límites siguientes:
-
![$\displaystyle {\lim_{x \rightarrow{2^{-}}}{\left[\frac{3+x}{x-2}+\frac{x-5}{\sqrt{2-x}}\right]}}$](img724.gif)
-
![$\displaystyle {\lim_{x \rightarrow{2^{-}}}{\left[\frac{3+x}{x-2}\cdot \frac{x-5}{\sqrt{2-x}}\right]}}$](img725.gif)
Ejemplo:
Calculemos:
 y y

Como
 entonces entonces
 además
además
 y y
 cuando cuando
 . Luego, se tiene que: . Luego, se tiene que:
 y y
 y aplicando el
teorema anterior tenemos que: y aplicando el
teorema anterior tenemos que:
![$\displaystyle {\lim_{x \rightarrow{2^{+}}}{\left[\frac{3x}{x-2}\cdot\frac{1-x}{x-2}\right]}=-\infty}$](img733.gif)
Ejercicio:
Calcule

Nota: los teoremas 12 a 18 son válidos cuando

Ejemplos:
-

-

-

-

-

Nota: observe que, como  está creciendo a través de valores
negativos es necesario que está creciendo a través de valores
negativos es necesario que  sea un número real, no
teniendo sentido expresiones como: sea un número real, no
teniendo sentido expresiones como:

Ejemplos:
-

-
![$\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{5+x^{\frac{1}{2}}}{x^{\frac{...
...rrow{-\infty}}{\left(\frac{5}{\sqrt[3]{x^{2}}}+\frac{1}{\sqrt[6]{x}}\right)}=0}$](img749.gif)
-

-

Note que si
 entonces entonces
 por lo que por lo que
 sí tiene sentido cuando sí tiene sentido cuando
 . .
Daremos ahora ejemplos de límites cuando
 y cuando y cuando
 . Para calcular . Para calcular
 y y
 factorizamos la variable de
mayor exponente como se evidencia a continuación. factorizamos la variable de
mayor exponente como se evidencia a continuación.
-



Note que
 cuando cuando

-



pues

-
 ejercicio para el estudiante
ejercicio para el estudiante
-



Recuerde que
 cuando cuando

-



Observe que evaluando, el numerador tiende a una constante (5), y el denominador
tiende a  . .
 (por teorema 19) (por teorema 19)
-
![$\displaystyle {\lim_{x \rightarrow{+\infty}}{[\sqrt{x^{2}+5x+1}-2x]}}$](img773.gif)
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\left[\sqrt{x^{2}\left(1+\frac{5}{x}+\frac{1}{x^{2}}\right)}-2x\right]}}$](img774.gif)
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\left[\sqrt{x^{2}}\sqrt{1+\frac{5}{x}+\frac{1}{x^{2}}}-2x\right]}}$](img775.gif)
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\left[\vert x\vert\sqrt{1+\frac{5}{x}+\frac{1}{x^{2}}}-2x\right] }}$](img776.gif)
Como  está definida a través de valores positivos
entonces está definida a través de valores positivos
entonces 
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\left[x\sqrt{1+\frac{5}{x}+\frac{1}{x^{2}}}-2x\right] }}$](img778.gif)
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{x\left[\sqrt{1+\frac{5}{x}+\frac{1}{x^{2}}}-2\right]}=-\infty}$](img779.gif)
Observe que
 y que la expresión dentro
del paréntesis tiende a y que la expresión dentro
del paréntesis tiende a  . .
-
![$\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{\sqrt[4]{3x^{4}+2x^{2}+1}-1}{2x-1}}}$](img781.gif)
![$=\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{\sqrt[4]{x^{4}(3+\frac{2}{x^{2}}+\frac{1}{x^{4}})}-1}{2x-1}}}$](img782.gif)
![$=\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{\vert x\vert\sqrt[4]{3+\frac{2}{x^{2}}+\frac{1}{x^{4}}}-1}{2x-1}}}$](img783.gif)
Como  crece a través de valores negativos se tiene que crece a través de valores negativos se tiene que

![$=\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{-x\sqrt[4]{3+\frac{2}{x^{2}}+\frac{1}{x^{4}}}-1}{2x-1}}}$](img785.gif)
![$=\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{x\left(-\sqrt[4]{3+\frac{2}{x^{2}}+\frac{1}{x^{4}}}-\frac{1}{x}\right)}{x(2-\frac{1}{x})}}}$](img786.gif)
![$=\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{-\sqrt[4]{3+\frac{2}{x^{2}}+\frac{1}{x^{4}}}-\frac{1}{x}}{2-\frac{1}{x}}=\frac{-\sqrt[4]{3}}{2}}}$](img787.gif)
Nota: Recuerde
![$\sqrt[n]{x^{n}}=\vert x\vert$](img788.gif) si si  es par. es par.
-
Ejercicio
![$\displaystyle {\lim_{x \rightarrow{-\infty}}{\frac{\sqrt[3]{5x^{3}+x^{2}-1}+2x}{3x^{2}+1}}}$](img789.gif)
-
![$\displaystyle {\lim_{x \rightarrow{+\infty}}{\frac{\sqrt[3]{x^{2}+1}-x}{\sqrt{x+2}-1}}}$](img790.gif)
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\frac{\sqrt[3]{x^{2}(1+\frac{1}{x^{2}})}-x}{\sqrt{x(1+\frac{2}{x})}-1}}}$](img791.gif)
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\frac{x^{\frac{2}{3}}\sqrt[3]{1+\frac{1}{x^{2}}}-x}{x^{\frac{1}{2}}\sqrt{1+\frac{2}{x}}-1}}}$](img792.gif)
![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\frac{x\left(\frac{1}{\sqrt[3]{x}...
...{2}}}-1\right)}{\sqrt{x}\left(\sqrt{1+\frac{2}{x}}-\frac{1}{\sqrt{x}}\right)}}}$](img793.gif)

Note que

-
![$\displaystyle {\lim_{x \rightarrow{+\infty}}{[\sqrt{2x^{2}+x+4}-\sqrt{2x^{2}+3x-2}]}}$](img796.gif)
Observe que:


Luego se presenta la forma
 para la que no
tenemos ningún teorema que nos permita dar el resultado. para la que no
tenemos ningún teorema que nos permita dar el resultado.
Cuando se presenta esta situación, primero racionalizamos y
luego evaluamos el límite con el proceso que ya conocemos:
Así tenemos que:




![$=\displaystyle {\lim_{x \rightarrow{+\infty}}{\frac{x(\frac{6}{x}-2)}{x\left[\sqrt{2+\frac{1}{x}+\frac{4}{x^{2}}}+\sqrt{2+\frac{3}{x}-\frac{2}{x^{2}}}\right]}}}$](img804.gif)


-
![$\displaystyle {\lim_{x \rightarrow{-\infty}}{(\sqrt{x^{2}-x}-\sqrt[3]{x^{3}+1})}}$](img807.gif)
Observe que:
 y y
![$\displaystyle {\lim_{x \rightarrow{-\infty}}{\sqrt[3]{x^{3}+1}}=\lim_{x \rightarrow{-\infty}}{x\sqrt[3]{1-\frac{1}{x^{2}}}}=-\infty}$](img809.gif)
Por lo que en este caso se presenta la forma
 , o sea, , o sea,
 para la que
sí existe un teorema y
concluimos que: para la que
sí existe un teorema y
concluimos que:
![$\displaystyle {\lim_{x \rightarrow{-\infty}}{(\sqrt{x^{2}-x}-\sqrt[3]{x^{3}+1})}=+\infty}$](img812.gif)
Ejercicio
-
 (respuesta: 2) (respuesta: 2)
Volver
Revista digital Matemática, Educación e Internet.
|