|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15 16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
Considere el caso particular 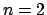 . Entonces . Entonces 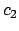 es la apotema de un cuadrado inscrito en un círculo de radio es la apotema de un cuadrado inscrito en un círculo de radio 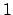 , que es igual a la mitad de la medida del lado , que es igual a la mitad de la medida del lado 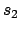 , es decir , es decir
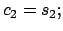 véase la figura 4: véase la figura 4:
|
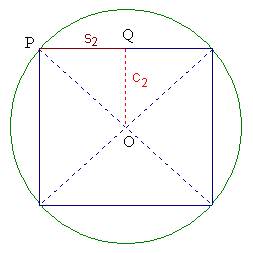
Figura 4 |
El triángulo 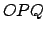 es rectángulo isósceles de hipotenusa es rectángulo isósceles de hipotenusa 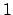 , por lo tanto aplicando el teorema de Pitagóras se obtiene , por lo tanto aplicando el teorema de Pitagóras se obtiene
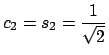 . Aunque geométricamente no tiene sentido hablar de . Aunque geométricamente no tiene sentido hablar de 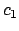 y y 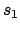 (pues no hay poligonos de (pues no hay poligonos de 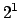 lados), se puede hallar una definición de estos de manera que las fórmulas de recurrencia sean válidas con lados), se puede hallar una definición de estos de manera que las fórmulas de recurrencia sean válidas con 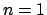 : :
y luego
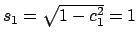 . Se define entonces . Se define entonces 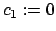 y y 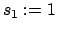 . .
|
![]()