|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15
16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
Se parte de la definición recursiva que se hizo de
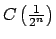 y y
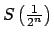 . Se definen para . Se definen para 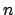 fijo: fijo:
y para 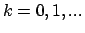 se define: se define:

Note que
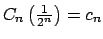 y y
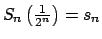 , tomando , tomando 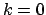 . En particular . En particular
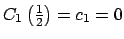 y y
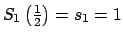 . .
Prueba
- La demostración de la identidad pitagórica se deja como ejercicio.
- Con
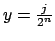 , se procede por inducción sobre , se procede por inducción sobre 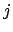 . Para . Para 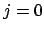 las igualdades son evidentes. En el paso inductivo, se asume que son válidas para las igualdades son evidentes. En el paso inductivo, se asume que son válidas para 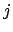 , y se demuestran para , y se demuestran para 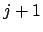 (donde (donde
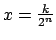 está fijo). Para hacer eso, se aplica primero la definición:
está fijo). Para hacer eso, se aplica primero la definición:
El primer término a la derecha es, por hipótesis de inducción:
mientras que el segundo es
Al restar y reagrupar estos términos se obtiene:
Esto demuestra la primera fórmula para 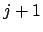 , y para la segunda se procede similarmente. , y para la segunda se procede similarmente.
- Como
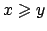 , aplicamos las identidades de la parte 2, con , aplicamos las identidades de la parte 2, con 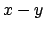 en vez de en vez de 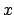 . Se obtiene . Se obtiene
Este es un sistema lineal en las variable
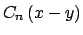 , ,
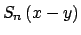 , cuya matriz es , cuya matriz es
Al resolver este sistema se obtienen las identidades deseadas. 
Tomando 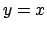 en la identidad 2 se obtiene el siguiente corolario. en la identidad 2 se obtiene el siguiente corolario.
Corolario 1
Para
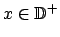 se tiene se tiene
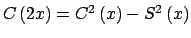 , ,
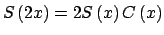 . .
Lema 3
Para cada 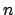 , , 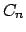 es una extensión de es una extensión de 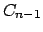 y y 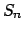 es una extensión de es una extensión de 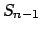 . .
Prueba
Note que
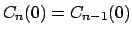 , y , y
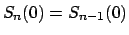 . Además, por el corolario anterior se tiene . Además, por el corolario anterior se tiene
y similarmente
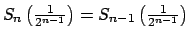 . Se debe demostrar que . Se debe demostrar que
para todo 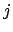 . Se aplicará inducción sobre . Se aplicará inducción sobre 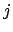 . Asumiendo que esto se cumple para cierto . Asumiendo que esto se cumple para cierto 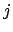 , se tiene: , se tiene:
Se ha usado aquí el teorema 2, y la hipótesis de inducción. Para 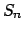 se procede de manera similar. se procede de manera similar. 
|
![]()
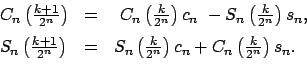
![]() y
y
![]() , tomando
, tomando ![]() . En particular
. En particular
![]() y
y
![]() .
.
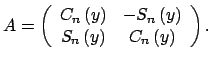
![]() en la identidad 2 se obtiene el siguiente corolario.
en la identidad 2 se obtiene el siguiente corolario.
![]() , y
, y
![]() . Además, por el corolario anterior se tiene
. Además, por el corolario anterior se tiene
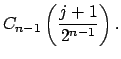
![]() se procede de manera similar.
se procede de manera similar. ![]()