|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15
16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
En general, cuando se quiere extender una función de un conjunto denso a todo
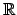 , es necesario que esta cumplan ciertas propiedades, como que sea continua o monótona. En la presente sección demostraremos que las funciones , es necesario que esta cumplan ciertas propiedades, como que sea continua o monótona. En la presente sección demostraremos que las funciones 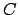 y y 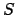 son monótonas en son monótonas en
![$ \left[ 0,\frac{1}{2}\right]$](img341.png) , y luego demostraremos que son continuas en el origen. Las propiedades demostradas arriba, nos ayudarán a deducir las correspondientes en el paso al límite. El resultado siguiente es de gran ayuda. , y luego demostraremos que son continuas en el origen. Las propiedades demostradas arriba, nos ayudarán a deducir las correspondientes en el paso al límite. El resultado siguiente es de gran ayuda.
Lema 4
Una función
![$ f:\mathbb{D}\cap \left[ 0,\frac{1}{2}\right] \rightarrow \mathbb{R}$](img342.png) es creciente si y solo si satisface lo siguiente: es creciente si y solo si satisface lo siguiente:
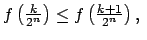 para para 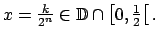 |
(9) |
Además, 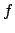 es estrictamente creciente si y solo si cumple (9), con desigualdad estricta. es estrictamente creciente si y solo si cumple (9), con desigualdad estricta.
Prueba
Es claro que si 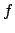 es creciente en es creciente en
![$ \mathbb{D}\cap \left[ 0,\frac{1}{2}\right] $](img346.png) , entonces saisface la propiedad (9). Recíprocamente, si , entonces saisface la propiedad (9). Recíprocamente, si 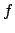 satisface (9), se toman satisface (9), se toman
![$ x,y\in \mathbb{D}\cap \left[ 0,\frac{1}{2}\right] $](img347.png) . Existen . Existen 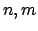 tales que tales que
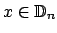 y y
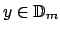 . Se puede asumir que . Se puede asumir que 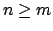 , en cuyo caso , en cuyo caso
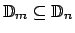 . Se tiene entonces que . Se tiene entonces que
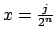 , ,
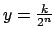 . Si . Si 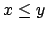 , entonces se tiene , entonces se tiene 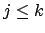 , y luego , y luego
La segunda parte se demuestra de manera casi idéntica, cambiando 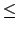 por por 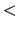 . .

Ahora recuerde que la sucesión
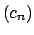 es creciente, y que es creciente, y que
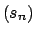 es decreciente. Se usará esto, y el lema anterior para demostrar que las funciones es decreciente. Se usará esto, y el lema anterior para demostrar que las funciones 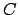 y y 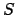 son monótonas en son monótonas en
![$ \left[ 0,\frac{1}{2}\right] \cap \mathbb{D}$](img358.png) , la primera decreciente y la segunda creciente. Para eso se demostrará por inducción que para cada , la primera decreciente y la segunda creciente. Para eso se demostrará por inducción que para cada
 se tiene: se tiene:
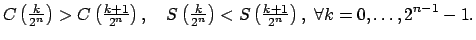 |
(10) |
Para 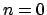 se debe mostrar que se debe mostrar que
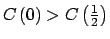 y y
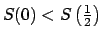 , lo cual es evidente. , lo cual es evidente.
Asumiendo que (10) es válida para 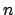 , se demostrará para , se demostrará para 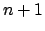 . Note que la hipótesis de inducción implica en particular que . Note que la hipótesis de inducción implica en particular que
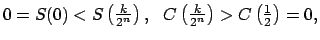 para para 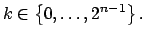 |
|
Sea
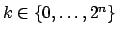 . Si . Si 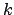 es impar, se tiene es impar, se tiene 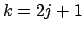 para algún para algún 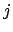 , y entonces , y entonces
Como
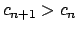 y y
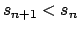 se sigue que se sigue que
Si 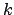 es par, se tiene es par, se tiene 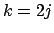 para algún para algún 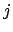 , y entonces , y entonces
Como 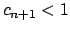 se tiene se tiene
En ambos casos se obtiene la desigualdad deseada para la función 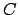 . Para . Para 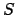 se procede de manera similar. Se ha demostrado que (10) se cumple para cada se procede de manera similar. Se ha demostrado que (10) se cumple para cada
 . Por el lema 4 se obtiene que . Por el lema 4 se obtiene que 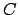 es decreciente estrictamente en cada es decreciente estrictamente en cada
![$ \mathbb{D}\cap \left[ 0,\frac{1}{2}\right] $](img346.png) , mientras que , mientras que 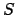 es estrictamente creciente en el mismo conjunto. En resumen: es estrictamente creciente en el mismo conjunto. En resumen:
Teorema 6
En
![$ \left[ 0,\frac{1}{2}\right] \cap \mathbb{D}$](img358.png) la función la función 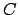 es estrictamente decreciente, mientras que la función es estrictamente decreciente, mientras que la función 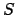 es estrictamente creciente. En particular se tiene es estrictamente creciente. En particular se tiene 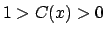 y y 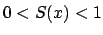 , para , para
![$ x\in \mathbb{D}\cap \left] 0,\frac{1}{2}\right[ $](img378.png) . .
Ahora recuerde que por el teorema 5 se tiene
Cuando 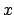 recorre recorre
![$ \mathbb{D}\cap \left[ 0,\frac{1}{2}\right] $](img346.png) , ,
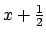 recorre recorre
![$ \mathbb{D}\cap \left[ \frac{1}{2},1\right] $](img381.png) . Como . Como  decrece en decrece en
![$ \mathbb{D}\cap \left[ 0,\frac{1}{2}\right] $](img346.png) , se sigue que , se sigue que
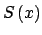 lo hace en lo hace en
![$ \mathbb{D}\cap \left[ \frac{1}{2},1\right] $](img381.png) . Por otro lado, como . Por otro lado, como 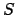 crece en crece en
![$ \mathbb{D}\cap \left[ 0,\frac{1}{2}\right] $](img346.png) , se sigue que , se sigue que
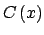 decrece en decrece en
![$ \mathbb{D}\cap \left[ \frac{1}{2},1\right] $](img381.png) . Las identidades . Las identidades
se pueden usar de la misma forma para deducir el comportamiento en el conjunto
![$ \mathbb{D}\cap \left[ 1,2\right] $](img385.png) . Finalmente, por ser estas funciones periódicas de período . Finalmente, por ser estas funciones periódicas de período 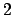 , el comportamiento en todo , el comportamiento en todo
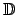 queda determinado por este teorema vía traslaciones. Por
ejemplo, la función queda determinado por este teorema vía traslaciones. Por
ejemplo, la función 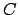 es estrictamente creciente en es estrictamente creciente en
![$ \mathbb{D}\cap \left[ 7,8\right] $](img386.png) , dado que , dado que
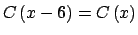 , y , y
![$ x-6\in \mathbb{D}\cap \left[ 1,2\right] $](img388.png) para para
![$ x\in \mathbb{D}\cap \left[ 7,8\right] $](img389.png) . .
|
![]()