Algunas identidades y desigualdades importantes

Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

Algunas identidades y desigualdades importantes

Recordemos que $\left( 2^{n}s_{n}\right)$ es una sucesión creciente que converge a $\pi$ , y por lo tanto debe tenerse en particular $2^{n}s_{n}\leq \pi$ , además es claro que $-\pi \leq 2^{n}s_{n}$ , así

$\displaystyle -\pi x\leq S\left( x\right) \leq \pi x,$ para $\displaystyle x=\frac{1}{2^{n}}.$

Esta desigualdad se sigue por inducción para todo 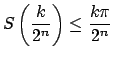$x\in \mathbb{D}^{+}$ . En efecto, si $S\left( \dfrac{k}{2^{n}}\right) \leq \dfrac{k\pi }{2^{n}}$ , se sigue que

$\displaystyle S\left( \frac{k+1}{2^{n}}\right) =S\left( \frac{k}{2^{n}}\right) ... ...eq \frac{k\pi }{2^{n}}+\frac{\pi }{2^{n}}=\frac{\left( k+1\right) \pi }{2^{n}},$

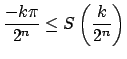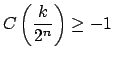donde usamos que $C\left( x\right) \leq 1$ para cada $x\in \mathbb{D}^{+}$ , y la hipótesis de inducción. Además, si $\dfrac{-k\pi }{2^{n}}\leq S\left( \dfrac{k}{2^{n}}\right)$ como $c_{n}\leq 1$ y $C\left( \dfrac{k}{2^{n}}\right) \geq -1$ , se tiene

$\displaystyle S\left( \frac{k}{2^{n}}\right) c_{n}\geq \dfrac{-k\pi }{2^{n}}c_{... ...quad s_{n}C\left( \dfrac{k}{2^{n}}\right) \geq -s_{n}\geq -\dfrac{\pi }{2^{n}},$

y por lo tanto

$\displaystyle S\left( \frac{k+1}{2^{n}}\right) =S\left( \frac{k}{2^{n}}\right) ... ...\left( \frac{k}{2^{n}}\right) s_{n}\geq -\dfrac{\left( k+1\right) \pi }{2^{n}}.$

Así, se obtiene el siguiente lema.

Lema 5 La función satisface $-\pi x\leq S\left( x\right) \leq \pi x$ , para cada $x\in \mathbb{D}^{+}$ .

Como es una función impar, la desigualdad se puede extender a $\mathbb{D}$ . En efecto, si $x\in \mathbb{D}^{-}$ , por el lema anterior $\pi x\leq S\left( -x\right) \leq -\pi x$ , por lo tanto

$\displaystyle \pi x\leq -S\left( -x\right) =S\left( x\right) \leq -\pi x.$

Sea ha demostrado el teorema siguiente.

Teorema 8 Para $x\in \mathbb{D}$ , se tiene que $\left\vert S\left( x\right) \right\vert \leq \pi \left\vert x\right\vert$ .

A continuación se presentan unas igualdades y desigualdades importantes para nuestros propósitos.

Teorema 9 Para $x,y\in \mathbb{D}$ se tiene

$\displaystyle S\left( x\right) -S\left( y\right)$	$\displaystyle =$	$\displaystyle 2C\left( \dfrac{x+y}{2}\right) S\left( \dfrac{x-y}{2}\right) ,\medskip\quad$
$\displaystyle C\left( x\right) -C\left( y\right)$	$\displaystyle =$	$\displaystyle 2S\left( \dfrac{x+y}{2}\right) S\left( \dfrac{y-x}{2}\right) .$

Prueba

Note que $x=\dfrac{x+y}{2}+\dfrac{x-y}{2}$ , $y=\dfrac{x+y}{2}-\dfrac{x-y}{2},$ al realizar esta sustitución en $S\left( x\right) -S\left( y\right)$ y aplicar el teorema 5 se obtiene el resultado para la función . El procedimiento es similar para la función .

Teorema 10 Para $x,y\in \mathbb{D}$ se tiene

$\displaystyle \left\vert S\left( x\right) -S\left( y\right) \right\vert \leq \p... ...ft( x\right) -C\left( y\right) \right\vert \leq \pi \left\vert x-y\right\vert .$

Prueba

Por los dos teoremas anteriores se tiene

$\displaystyle \left\vert S\left( x\right) -S\left( y\right) \right\vert =2\left... ... S\left( \dfrac{x-y}{2}\right) \right\vert \leq \pi \left\vert x-y\right\vert .$

Para

se procede de manera similar. $\Box$

En secciones anteiores se demostró que $\left( \dfrac{2^{n}s_{n}}{c_{n}}\right) =\left( \dfrac{Q_{n}}{2}\right)$ es una sucesión decreciente que converge a $\pi$ , por lo tanto

$\displaystyle \dfrac{S\left( x\right) }{C\left( x\right) }\geq \pi x,$ para $\displaystyle x=\dfrac{1}{2^{n}}.$

(11)

Ahora se procederá a extender esta desigualdad a $\mathbb{D\cap }\left[0,\frac{1}{2}\right[$ . La siguiente definición nos ayudará a simplificar la notación. Se define la función

$\displaystyle T\left( x\right) =\dfrac{S\left( x\right) }{C\left( x\right) },$ para $\displaystyle x\in$ Dom $\displaystyle (T)=\mathbb{D-}\left\{ n+\frac{1}{2}:n\in \mathbb{Z}\right\} .$

Note que

$\displaystyle T\left( x+y\right) =\dfrac{S\left( x\right) C\left( y\right) +C\l... ...ight) }{C\left( x\right) C\left( y\right) -S\left( x\right) S\left( y\right) },$

dividiendo numerador y denominador en la desigualdad anterior entre $C\left(x\right) C\left( y\right)$ , se obtiene el siguiente lema:

Lema 6 Si $x,y,x+y\in$ Dom, se tiene

$\displaystyle T\left( x+y\right) =\dfrac{T\left( x\right) +T\left( y\right) }{1-T\left(x\right) T\left( y\right) }.$

Además, como es estrictamente creciente y estrictamente decreciente en $\mathbb{D}\cap \left[ 0,\frac{1}{2}\right[$ , se sigue que es estrictamente creciente en dicho conjunto. En efecto, si $0\leq x<y<\frac{1}{2}$ , se tiene

$\displaystyle 0\leq T\left( x\right) =\dfrac{S\left( x\right) }{C\left( x\right) }<\frac{S\left( y\right) }{C\left( y\right) }.$

En particular, para $x\in \mathbb{D}\cap \left[ 0,\frac{1}{4}\right[$ se tiene $0\leq T\left( x\right) <T\left( \frac{1}{4}\right) =1$ , y por lo tanto

$\displaystyle 0<1-T\left( x\right) T\left( y\right) \leq 1,$ para $\displaystyle x,y\in \mathbb{D}\cap \left[ 0,\tfrac{1}{4}\right[ .$

(12)

Por lo tanto se concluye para $x,y\in \mathbb{D}\cap \left[ 0,\frac{1}{4}\right[$ :

$\displaystyle T\left( x+y\right) =\dfrac{T\left( x\right) +T\left( y\right) }{1-T\left(x\right) T\left( y\right) }\geq T\left( x\right) +T\left( y\right) .$

Con este resultado se probará el siguiente lema.

Lema 7 La función satisface $\left\vert T\left( x\right) \right\vert \geq \pi \left\vert x\right\vert$ , para cada $x\in \mathbb{D}\cap \left[ -\frac{1}{4},\frac{1}{4}\right]$ .

Prueba

Si $0\leq x=\dfrac{k}{2^{n}}<\dfrac{1}{4}$ , se procede por inducción sobre . En el paso induccitivo se tiene que para $\frac{k+1}{2^{n}}\leq \dfrac{1}{4}$ , utilizando la desigualdad anterior, la hipótesis inductiva y (11), se obtiene

$\displaystyle T\left( \dfrac{k+1}{2^{n}}\right) \geq T\left( \dfrac{k}{2^{n}}\r... ...\dfrac{k\pi }{2^{n}}+\dfrac{\pi }{2^{n}}=\dfrac{\left( k+1\right) \pi }{2^{n}}.$

Si $x\in \mathbb{D}\cap \left[ \dfrac{-1}{4},0\right]$ , entonces por el lema anterior $-T\left( x\right) =T\left( -x\right) \geq -\pi x$ , de donde se obtiene que $T\left( x\right) \leq \pi x\leq 0$ , y de ahí el resultado. $\Box$