Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15  16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

 

Construcción de las funciones $ S$ y $ C$ en el conjunto $ \mathbb{D}$

Sea $ \mathbb{D}_{1}=\left\{ \dfrac{1}{2^{n}}:n\in \mathbb{N}\right\} $. Se definen las funciones $ C:\mathbb{D}_{1}\rightarrow \mathbb{R}$ y $ \ S: \mathbb{D}_{1}\rightarrow \mathbb{R}$, de la siguiente manera:

$\displaystyle C\left( \tfrac{1}{2^{n}}\right) =c_{n},\qquad \qquad S\left( \tfrac{1}{2^{n}} \right) =s_{n}.$    

De acuerdo con las propiedades de las sucesiones obtenidas anteriormente, se deducen algunas identidades:

  1. Dado que $ s_{n}^{2}+c_{n}^{2}=1$ se tiene $ C^{2}\left( \tfrac{1}{2^{n}}\right) +S^{2}\left( \tfrac{1}{2^{n}}\right) =1$, es decir

    $\displaystyle C^{2}\left( x\right) +S^{2}\left( x\right) =1,$ para $\displaystyle x\in \mathbb{D}_{1}.$    

  2. Similarmente se tiene $ C^{2}\left( \tfrac{1}{2^{n}}\right)-S^{2}\left( \tfrac{1}{2^{n}}\right) =C\left( \tfrac{1}{2^{n-1}}\right) $, debido a que $ c_{n}^{2}-s_{n}^{2}=c_{n-1}$. Esto es, para $ x\in \mathbb{D}_{1}$ se tiene:

    $\displaystyle C^{2}\left( x\right) -S^{2}\left( x\right) =C\left( 2x\right) .$    

  3. La igualdad $ s_{n-1}=2s_{n}c_{n}$ se convierte en $ S\left( \tfrac{1}{2^{n-1}}\right) =2\cdot S\left( \tfrac{1}{2^{n}}\right) \cdot C\left( \tfrac{1}{2^{n}}\right) $, es decir

    $\displaystyle S\left( 2x\right) =2\cdot S\left( x\right) \cdot C\left( 2x\right) ,$ para $\displaystyle x\in \mathbb{D}_{1}.$    

Se intentará definir $ C\left( \frac{k}{2^{n}}\right) $ y $ S\left( \frac{k}{2^{n}}\right) $ por inducción sobre $ k$. Lo más conveniente sería:

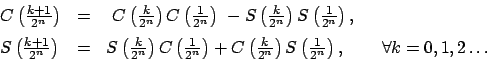\begin{displaymath}\begin{array}{llll} C\left( \frac{k+1}{2^{n}}\right) & = & \ ... ...c{1}{2^{n}}\right) ,\ \quad & \forall k=0,1,2\ldots \end{array}\end{displaymath}    

Esta definición sin embargo requiere de ciertos cuidados. Por ejemplo, cuando $ k=n=2$, volvemos a definir $ C\left( \tfrac{1}{2}\right) $, que ya se había definido con $ k=n=1$. En general, en el paso $ n$, se redefinen todos los valores que se habían definido en el paso $ n-1$. Debemos entonces verificar que la nueva definición coincide con la anterior, en cada paso. Para evitar problemas de notación en este sentido, es mejor adoptar el siguiente enfoque: $ \medskip$

Definimos primero, para cada $ n$, funciones $ C_{n}$ y $ S_{n}$ de acuerdo con la definición recursiva que se tiene, en el conjunto

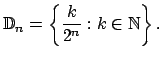$\displaystyle \mathbb{D}_{n}=\left\{ \dfrac{k}{2^{n}}:k\in \mathbb{N}\right\} .$    

Luego se verificará que para cada $ n$, $ C_{n}$ extiende a $ C_{n-1}$, y $ S_{n}$ extiende a $ S_{n-1}$.

Finalmente se definirán $ C$ y $ S$ en el conjunto

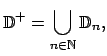$\displaystyle \mathbb{D}^{+}=\bigcup_{n\in \mathbb{N}}\mathbb{D}_{n},$    

como la "unión" de estas funciones.


 

Revista Virtual Matemática, Educación e Internet

Derechos Reservados