|
Inicio
1 2
3 4 5
6 7 8
9 10 11
12 13
14 15
16 17
18 19 20
21
22 23 24
25 26
27 28 29
30 31
32 33 34
35 36
37 38
Las desigualdades obtenidadas enunciadas en el teorema 10, nos inducen a una única manera de definir las funciones 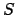 y y 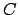 en en
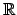 . En efecto, primeramente si . En efecto, primeramente si
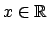 , y , y
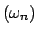 es una sucesión en es una sucesión en
 convergente a convergente a  , entonces , entonces
 es una sucesión de Cauchy, es decir: es una sucesión de Cauchy, es decir:
Por la desigualdad dada en el teorema 10, se sigue que
así que la sucesión
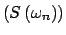 es de Cauchy, y por lo tanto convergente en es de Cauchy, y por lo tanto convergente en
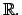
Por otro lado, si
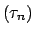 es otra sucesión de diádicos que converge a es otra sucesión de diádicos que converge a 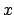 , entonces , entonces
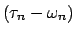 es una sucesión en es una sucesión en
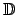 que converge a 0, y luego que converge a 0, y luego
Esto demuestra que
Lo anterior demuestra que el valor del límite de la sucesión
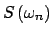 , es independiente de la sucesión de diádicos que se escoja, siempre que esta converja a , es independiente de la sucesión de diádicos que se escoja, siempre que esta converja a 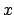 . Resumimos: . Resumimos:
Teorema 11
Existe un número real 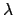 tal que, para toda sucesión tal que, para toda sucesión
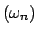 de diádicos que converge a de diádicos que converge a 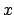 , se tiene que la sucesión , se tiene que la sucesión
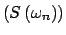 converge a converge a 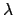 . .
Por lo tanto tiene sentido definir
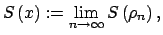 para cualquier sucesión para cualquier sucesión 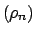 en en 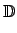 convergente a convergente a 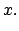 |
|
Para
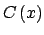 , se procede de manera similar, se obtiene que se debe definir , se procede de manera similar, se obtiene que se debe definir
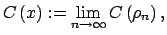 para cualquier sucesión para cualquier sucesión 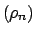 en en 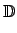 convergente a convergente a 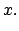 |
|
Nótese que la definición de 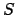 (y por ende la de (y por ende la de 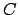 ) es consistente con la definición que ya se tenía para ) es consistente con la definición que ya se tenía para
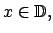 puesto que en tal caso se puede tomar puesto que en tal caso se puede tomar
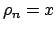 para todo para todo
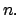
Nótese que la definición de 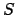 (y similarmente la de (y similarmente la de 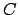 ) es la única posible, si se quiere que esta función sea continua en ) es la única posible, si se quiere que esta función sea continua en
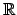 . En la siguiente sección, se demuestra que también es la única posible, si se quiere que . En la siguiente sección, se demuestra que también es la única posible, si se quiere que 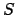 sea creciente en sea creciente en
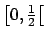 . .
|
![]()